13 câu hỏi trắc nghiệm thuộc Dạng 1. Tìm giao tuyến của hai mặt phẳng sử dụng quan hệ song song có đáp án

Bài tập chuyên đề toán 11 Bài 2: Hai đường thẳng chéo nhau có đáp án

Dạng 1. Tìm giao tuyến của hai mặt phẳng sử dụng quan hệ song song có đáp án

125 lượt thi
13 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)

Xem đáp án

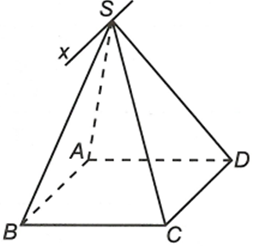
Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD) (ảnh 1)

Ta có $\{\begin{cases} (S A B) \cap (S C D) = S \\ A B \subset (S A B), C D \subset (S C D) \\ A B / / C D \end{cases}$

Suy ra

(S A B) \cap (S C D) = S x

với

S x / ​ / A B / ​ / C D

Câu 2:

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), đáy lớn AB. Cho M là điểm bất kì thuộc cạnh SC. Tìm giao tuyến của các mặt phẳng:

a) $(S A B) \cap (S C D)$

Xem đáp án

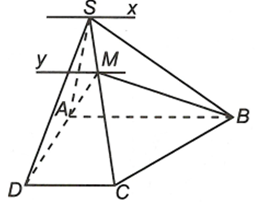
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), đáy lớn AB. Cho M là điểm bất kì thuộc cạnh SC. (ảnh 1)

a) Ta có $(S A B) \cap (S C D) = S$ , mà AB // CD

Suy ra $(S A B) \cap (S C D) = S x$ , trong đó $S x / / A B / / C D$

Câu 3:

b) $(S C D) \cap (M A B)$

Xem đáp án

b) Do $M \in S C$ nên $(S C D) \cap (M A B) = M$ , mặt khác AB // CD

$\Rightarrow (S C D) \cap (M A B) = M y$ , trong đó My // AB // CD

Câu 4:

Cho tứ diện SABC. Gọi G, I lần lượt là trọng tâm của tam giác ABC và SAB. Tìm giao tuyến của mặt phẳng (AIG) và mặt phẳng (SAC)

Xem đáp án

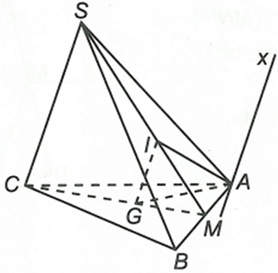
Cho tứ diện SABC. Gọi G, I lần lượt là trọng tâm của tam giác ABC và SAB. Tìm giao tuyến của mặt phẳng (AIG) và mặt phẳng (SAC) (ảnh 1)

Gọi M là trung điểm của AB.

Do I là trọng tâm của tam giác SAB suy ra $\frac{M I}{M S} = \frac{1}{3}$

Tương tự ta có $\frac{M G}{M C} = \frac{1}{3}$

Suy ra $\frac{M I}{M S} = \frac{M G}{M B} \Rightarrow G I / / S C$

Từ đó ta có $(S A C) \cap (A I G) = A x$ , trong đó Ax // SC // GI

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.

a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAC) và (SBD)

Xem đáp án

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (ảnh 1)

a) Ta có $\{\begin{cases} S \in (S A B) \cap (S C D) \\ A B \subset (S A B); C D \subset (S C D) \\ A B / / C D \end{cases}$

$\Rightarrow (S A B) \cap (S C D) = S x$ trong đó Sx // AB // CD

Trong (ABCD) gọi $\{O\} = A C \cap B D$ , suy ra $O \in (S A C) \cap (S B D) (1)$

Lại có $S \in (S A C) \cap (S B D) (2)$

Từ (1) và (2), suy ra $S O = (S A C) \cap (S B D)$

Câu 6:

b) Gọi M là trung điểm BC, đường thẳng d qua M và song song SD.

Tìm giao điểm của d và mặt phẳng (SAB)

Xem đáp án

b) Vì d qua M và song song SD nên $d \subset (S D M)$

Lại có $S \in (S D M) \cap (S A B)$

Trong (ABCD) có $\{I\} = A B \cap D M$ suy ra $I \in (S D M) \cap (S A B)$

Khi đó $(S D M) \cap (S A B) = S I$

Trong (SDM) có $\{N\} = S I \cap d$ suy ra $N = d \cap (S A B)$

Câu 7:

Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Tìm giao tuyến của hai mặt phẳng (ABD) và (MNP)

Xem đáp án

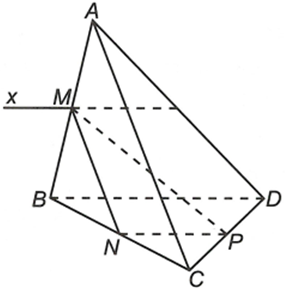
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Tìm giao tuyến của hai mặt phẳng (ABD) và (MNP) (ảnh 1)

Ta có $M \in A B$ nên $M \in (A B D) \cap (M N P)$

Xét ∆BCD, có NP là đường trung bình => NP // BD

Từ đó suy ra $(A B D) \cap (M N P) = M x$ , trong đó Mx // NP // BD

Câu 8:

Cho hình chóp S.ABCD có đáy là hình thang (AB // CD). Gọi I, J lần lượt là trung điểm của AD và BC, G là trọng tâm tam giác SAB. Giao tuyến của (SAB) và (IJG) là

A. SC

B. đường thẳng qua S và song song với AB

C. đường thẳng qua G và song song với CD

D. đường thẳng qua G và cắt BC

Xem đáp án

Đáp án C

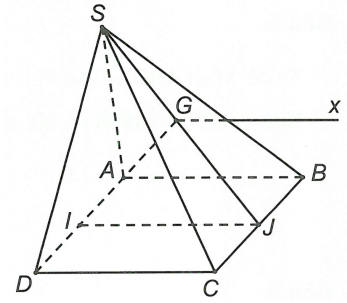
Cho hình chóp S.ABCD có đáy là hình thang (AB // CD). Gọi I, J lần lượt là trung điểm của AD và BC, G là trọng tâm tam giác SAB. (ảnh 1)

Ta có $\{\begin{cases} G \in (G A B) \cap (G I J) \\ A B / / I J \end{cases} \Rightarrow (G A B) \cap (G I J) = G x$ sao cho Gx // AB // IJ.

Mà AB // CD => Gx // AB // IJ // CD

Câu 9:

Cho tứ diện ABCD, gọi I, J và K lần lượt là trung điểm của AB, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là

A. KD

B. KI

C. đường thẳng đi qua K và song song với AB

D. không có

Xem đáp án

Đáp án B

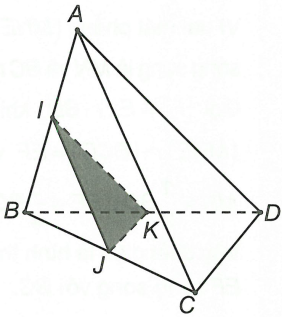
Cho tứ diện ABCD, gọi I;,J và K lần lượt là trung điểm của AB, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là (ảnh 1)

Ta có $I \in A B \subset (A B D)$ nên I là điểm chung của hai mặt phẳng (ABD) và (IJK)

Tương tự có K là điểm chung của hai mặt phẳng (ABD) và (IJK). Vậy giao tuyến là KI

Câu 10:

Cho hình chóp S.ABCD có đáy là ABCD hình thang (AB // CD). Giao tuyến của hai mặt phẳng (SAB) và (SCO) là

A. đường thẳng qua S và song song với AB và CD

B. đường thẳng qua S và song song với AD và BC

C. đường thẳng qua S và giao điểm của AD và CD

D. đường thẳng qua S và giao điểm của AC và BD

Xem đáp án

Đáp án A

Cho hình chóp S.ABCD có đáy là ABCD hình thang (AB // CD). Giao tuyến của hai mặt phẳng (SAB) và (SCO) là (ảnh 1)

Ta có $\{\begin{cases} S \in (S A B), S \in (S C D) \\ A B / / C D \end{cases} \Rightarrow$ giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng đi qua S và song song với AB; CD

Câu 11:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CD. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với

A. AD

B. BJ

C. BI

D. IJ

Xem đáp án

Đáp án D

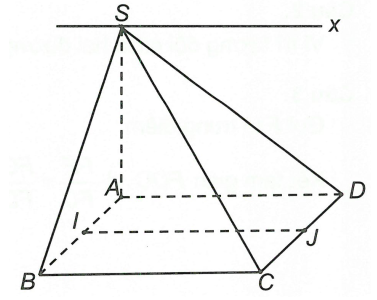
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CD. (ảnh 1)

Ta có: $\{\begin{cases} S \in (S A B) \cap (S C D) \\ A B / / C D \end{cases} \Rightarrow$ giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng đi qua S và song song với AB. Mà I, J lần lượt là trung điểm của AB và CD nên IJ // AB.

Vậy giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng qua S và song song với IJ

Câu 12:

Cho tứ diện ABCD, gọi (M không trùng với A, B). N và K lần lượt là trung điểm BC, CD. Giao tuyến của (ABD) và (MNK) là

A. MN

B. MD

C. MC

D. Mx song song với BD và NK

Xem đáp án

Đáp án D

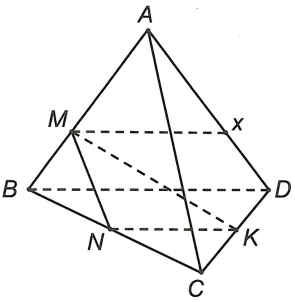
Cho tứ diện ABCD, gọi (M không trùng với A, B). N và K lần lượt là trung điểm BC, CD. Giao tuyến của (ABD) và (MNK) là (ảnh 1)

Ta có $M \in (A B D) \cap (M N K)$ và CD // NK

Nên $(A B D) \cap (M N K) = M x$ sao cho Mx // DB // NK

Câu 13:

Cho tứ diện ABCD, gọi M và N lần lượt là trung điểm của AB và AC. E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là

A. tam giác MNE

B. tứ giác MNEFvớ\ F là điểm bất kì trên cạnh BD

C. hình bình hành MNEF với F là điểm bất kì trên cạnh BD mà EF song song với BC

D. hình thang MNEF với F là điểm trên cạnh BD mà EF song song với BC

Xem đáp án

Đáp án D

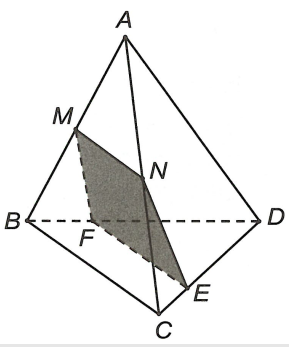
Cho tứ diện ABCD, gọi M và N lần lượt là trung điểm của AB và AC. E là điểm trên cạnh CD với ED = 3EC (ảnh 1)

Ta có $(M N E) \cap (A B C) = M N, (M N E) \cap (A C D) = N E$

Vì hai mặt phẳng (MNE) và (BCD) lần lượt chứa hai đường thẳng song song là MN và BC nên $(M N E) \cap (B C D) = E x$ sao cho Ex // BC.

Gọi $\{F\} = E x \cap B D$ , khi đó

$(M N E) \cap (B C D) = E F$ và $(M N E) \cap (A B D) = F M$ và $M N = \frac{1}{2} B C; E F = \frac{3}{4} B C$

Vậy thiết diện là hình thang MNEF với F là điểm trên cạnh BD mà EF song song với BC.

Bắt đầu thi ngay

Bài tập chuyên đề toán 11 Bài 2: Hai đường thẳng chéo nhau có đáp án

Dạng 1. Tìm giao tuyến của hai mặt phẳng sử dụng quan hệ song song có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương