14 câu hỏi trắc nghiệm thuộc Dạng 2: Chứng minh hai đường thẳng song song có đáp án

Câu 1:

Cho tứ diện ABCD. Gọi M, N là trung điểm của AB, BC và P là điểm nằm trên cạnh CD. Gọi Q là giao điểm của DA với mặt phẳng (MNP). Chứng minh PQ // MN và PQ // AC

Xem đáp án

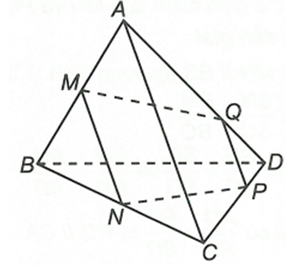
Cho tứ diện ABCD. Gọi M, N là trung điểm của AB, BC và P là điểm nằm trên cạnh CD. Gọi Q là giao điểm của DA với mặt phẳng (MNP). (ảnh 1)

Ta có $C D \cap (M N P) = \{P\}$ và MN // AC

Suy ra $(M N P) \cap (A C D) = P x$

Trong đó Px // MN // AC

Mặt khác $D A \cap (M N P) = \{Q\}$ nên $Q \in P x$

Vậy PQ // MN // AC

Câu 2:

Cho hình chóp S.ABCD đáy ABCD là hình thang với cạnh đáy AB và CD $(A B > C D)$ . Gọi M, N lần lượt là trung điểm của SA, SB.

a) Chứng minh MN // CD

Xem đáp án

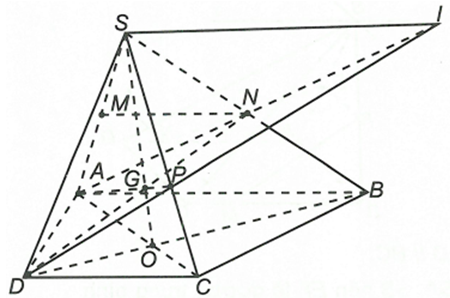
Cho hình chóp S.ABCD đáy ABCD là hình thang với cạnh đáy AB và CD (AB > CD) a) Chứng minh MN // CD (ảnh 1)

a) Ta có MN là đường trung bình của tam giác SAB suy ra MN // AB. Mà AB // CD nên MN // CD

Câu 3:

b) Tìm giao điểm P của SC và mặt phẳng (AND). Kéo dài AN và DP cắt nhau tại I.

Chứng minh SI // AB // CD

Xem đáp án

b) Gọi $\{O\} = A C \cap B D, \{G\} = S O \cap D N$ và $\{P\} = A G \cap S C$

suy ra $\{P\} = S C \cap (A D N)$

Ta có AB // CD nên $(S A B) \cap (S C D) = S x$ sao cho Sx // AB // CD

Theo đầu bài $\{I\} = A N \cap D P$ nên $I \in (S A B)$ và $I \in (S C D) \Rightarrow I \in S x$

Từ đó ta có SI // AB // CD

Câu 4:

Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi M, N, P, Q là các điểm lần lượt trên BC, SC, SD, AD sao cho MN // BS, NP // CD, MQ // CD

a) Chứng minh PQ // SA

Xem đáp án

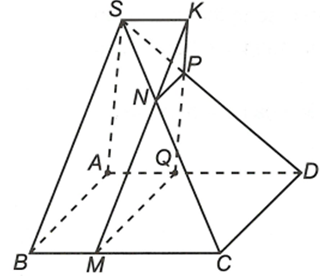
Cho hình chóp S.ABCD đáy ABCD là hình bình hành. sao cho MN // BS, NP // CD, MQ // CD a) Chứng minh PQ // SA (ảnh 1)

a) Ta có MN // BS áp dụng định lý Ta-lét ta được $\frac{S N}{S C} = \frac{B M}{B C}$

Tương tự $\frac{S N}{S C} = \frac{S P}{S D}$ và $\frac{B M}{B C} = \frac{A Q}{A D}$

Từ đó ta có

\frac{A Q}{A D} = \frac{S P}{S D} \Rightarrow P Q / ​ / S A

Câu 5:

b) Gọi K là giao điểm của MN và PQ. Chứng minh SK // SD // BC

Xem đáp án

b) Do AD // BC nên $(S A D) \cap (S B C) = S x$ trong đó Sx // AD // BC

Mặt khác $\{K\} = M N \cap Q P$ nên K là điểm chung của hai mặt phẳng (SAD) và (SBC) suy ra $K \in S x$

Vậy Sx // AD // BC

Câu 6:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. $S A = S B = a, S C = S D = a \sqrt{3}$ . Gọi E, G lần lượt là trung điểm của SA và SB. M là điểm tùy ý trên cạnh BC (không trùng với B, C).

a) Xác định giao tuyến của các mặt phẳng (SAB) và (SCD); (SAD) và (SBC)

Xem đáp án

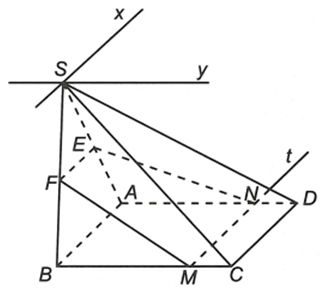
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. a) Xác định giao tuyến của các mặt phẳng (SAB) và (SCD); (SAD) và (SBC) (ảnh 1)

a) Ta có

$\{\begin{cases} S \in (S A D) \cap (S C D) \\ A B / / C D, A B \subset (S A B), C D \subset (S C D) \end{cases}$

$\Rightarrow (S A B) \cap (S C D) = S x$ , trong đó Sx // AB // CD

Tương tự $\{\begin{cases} S \in (S A D) \cap (S B C) \\ A D / / B C, A D \subset (S A D), B C \subset (S B C) \end{cases}$

$\Rightarrow (S A D) \cap (S B C) = S y$ , trong đó Sy // AD // BC.

Câu 7:

b) Xác định giao tuyến của các mặt phẳng (MEF) và (ABCD)

Xem đáp án

b) Do E, F lần lượt là trug điểm của SA, SB nên EF là đường trung bình của ∆SAB

Do đó EF // AB và $E F = \frac{1}{2} A B$

Ta có $\{\begin{cases} M \in (M E F) \cap (A B C D) \\ E F / / A B \\ E F \subset (M E F), A B \subset (A B C D) \end{cases}$

$\Rightarrow (M E F) \cap (A B C D) = M t$ trong đó Mt // AB // CD hay $(M E F) \cap (A B C D) = M N$

( với $A D \cap M t = \{N\}$ và MN // AB // CD).

Câu 8:

Cho hình chóp S.ABC. Gọi G và G' lần lượt là trọng tâm của tam giác ABC và tam giác SBC. Chứng minh GG' song song với SA.

Xem đáp án

Cho hình chóp S.ABC. Gọi G và G' lần lượt là trọng tâm của tam giác ABC và tam giác SBC. Chứng minh GG' song song với SA. (ảnh 1)

Gọi M là trung điểm của BC nên $\frac{M G}{M A} = \frac{1}{3}; \frac{M G^{'}}{M S} = \frac{1}{3}$ (tính chất của trọng tâm).

Xét ∆SAM, có $\frac{M G}{M A} = \frac{M G^{'}}{M S}$ theo định lí Ta-lét đảo suy ra GG’ // SA

Câu 9:

Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của mặt phẳng (SAD) và mặt phẳng (SBC) là đường thẳng song song với đường thẳng nào sau đây

A. AD

B. BD

C. AC

D. SC

Xem đáp án

Đáp án A

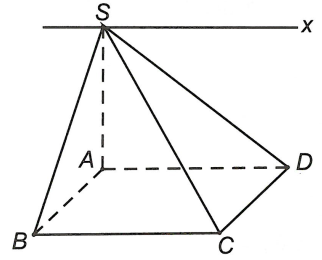
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của mặt phẳng (SAD) và mặt phẳng (SBC) là đường thẳng song song với đường thẳng nào sau đây (ảnh 1)

Ta có $\{\begin{cases} S \in (S A D) \cap (S B C) \\ A D / / B C \end{cases}$

$\Rightarrow (S A D) \cap (S B C) = S x$ sao cho Sx // AD // BC

Câu 10:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau

B. Hai đường thẳng không có điểm chung thì chéo nhau

C. Hai đường thẳng chéo nhau thì không có điểm chung

D. Hai đường thẳng phân biệt không song song thì chéo nhau

Xem đáp án

Đáp án C

Vị trí tương đối giữa hai đường thẳng chéo nhau thì không có điểm chung

Câu 11:

Cho tứ diện ABCD, gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng?

A. GE và CD chéo nhau

B. GE // CD

C. GE cắt AD

D. GE cắt CD

Xem đáp án

Đáp án B

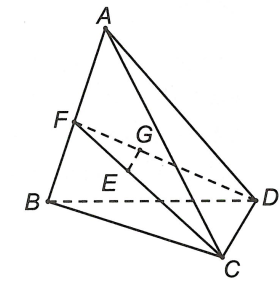
Cho tứ diện ABCD, gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng? (ảnh 1)

Gọi F là trung điểm

Xét tam giác FDC vì $\frac{F E}{F C} = \frac{F G}{F D} = \frac{1}{3}$ nên EG // CD

Câu 12:

Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là CD. Gọi M là trung điểm của SA, N là giao điểm của cạnh SB và mặt phẳng (MCD). Mệnh đề nào sau đây đúng?

A. MN và SD cắt nhau

B. MN // CD

C. MN và SC cắt nhau

D. MN và CD chéo nhau

Xem đáp án

Đáp án B

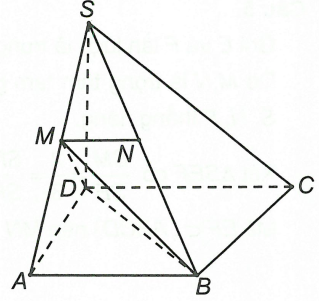
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là CD. Gọi M là trung điểm của SA, N là giao điểm của cạnh SB và mặt phẳng (MCD). (ảnh 1)

Ta có: $\begin{array}{l} M N = (M C D) \cap (S A B) \\ A B \subset (S A B) \\ C D \subset (M C D) \\ A B / / C D \end{array}\} \Rightarrow M N / / C D$

Câu 13:

Cho hình chóp S.ABCD. Gọi I, J lần lượt là trung điểm của AB và BC. Giao tuyến của hai mặt phẳng (SAC) và (SIJ) là một đường thẳng song song với

A. đường thẳng AD

B. đường thẳng AB

C. đường thẳng AC

D. đường thẳng BD

Xem đáp án

Đáp án A

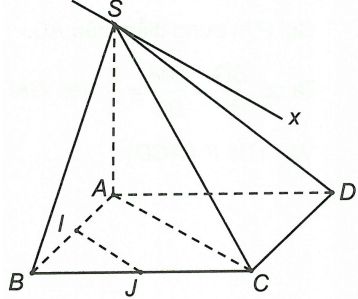
Cho hình chóp S.ABCD. Gọi I, J lần lượt là trung điểm của AB và BC. Giao tuyến của hai mặt phẳng (SAC) và (SIJ) là một đường thẳng song song với (ảnh 1)

Xét hai mặt phẳng (SAC) và (SIJ) ta có S là điểm chung IJ // AC (đường trung bình trong tam giác).

Suy ta giao tuyến của hai mặt phẳng (SAC) và (SIJ) là một đường thẳng qua S song song với AC

Câu 14:

Cho tứ diện ABCD. Có bao nhiêu cặp đường thẳng chéo nhau?

A. 3

B. 4

C. 5

D. 2

Xem đáp án

Đáp án C

Các cặp đường thẳng chéo nhau trong tứ diện ABCD là: AB và CD; AD và BC; AC và BD

Bài tập chuyên đề toán 11 Bài 2: Hai đường thẳng chéo nhau có đáp án

Dạng 2: Chứng minh hai đường thẳng song song có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương