25 câu hỏi trắc nghiệm thuộc Chủ đề 2: Góc Dạng 3. Góc giữa hai mặt phẳng

Câu 1:

S A ⊥ (A B C)

và

A B ⊥ B C,

gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?

A. $\hat{S B A} .$

B. $\hat{S C A} .$

C. $\hat{S C B} .$

D. $\hat{S I A} .$

Xem đáp án

Chọn đáp án A

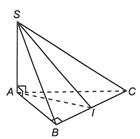
Cho hình chóp S.ABC có SA vuông góc (ABC) và AB vuông góc BC, gọi I là trung điểm BC. Góc (ảnh 1)

Ta có: $B C ⊥ S A, B C ⊥ A B \Rightarrow B C ⊥ S B .$

Suy ra $\{\begin{cases} (S B C) \cap (A B C) = B C \\ A B ⊥ B C, A B \subset (A B C) \\ S B ⊥ B C, S B \subset (S B C) \end{cases}$

$\Rightarrow \hat{((S B C), (A B C))} = \hat{(A B, S B)} = \hat{S B A} .$

Câu 2:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và

S A ⊥ (A B C D) .

Gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?

A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc $\hat{A B S} .$

B. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc $\hat{S O A} .$

C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc $\hat{S D A} .$

D. $(S A C) ⊥ (S B D) .$

Xem đáp án

Chọn đáp án C.

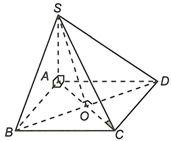
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc (ABCD). Gọi O là tâm hình vuông (ảnh 1)

Ta có $\{\begin{cases} (S A D) \cap (A B C D) = A D \\ A B ⊥ A D, A B \subset (A B C D) \\ S A ⊥ A D, S A \subset (S A D) \end{cases}$

$\Rightarrow \hat{((S A D), (A B C D))} = \hat{(S A, A B)} = \hat{S A B} .$

Câu 3:

Cho hình chóp S.ABC có

S A ⊥ (A B C)

và đáy ABC vuông ở A. Khẳng định nào sau đây sai?

A. $(S A B) ⊥ (A B C) .$

B. $(S A B) ⊥ (S A C) .$

C. Vẽ $A H ⊥ B C, H \in B C$ thì $\hat{A H S} = \hat{((S B C), (A B C))} .$

D. Góc giữa hai mặt phẳng (SBC) và (SAC) là góc $\hat{S C B} .$

Xem đáp án

Chọn đáp án D.

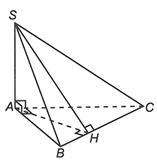
Cho hình chóp S.ABC có SA vuông góc (ABC) và đáy ABC vuông ở A. Khẳng định nào sau đây sai? (ảnh 1)

+) $S A ⊥ (A B C) \Rightarrow (S A B) ⊥ (A B C)$ nên đáp án A đúng.

+) $A B ⊥ A C, A B ⊥ S A \Rightarrow A B ⊥ (S A C)$

$\Rightarrow (S A B) ⊥ (S A C)$ nên đáp án B đúng.

+) $A H ⊥ B C; B C ⊥ S A \Rightarrow B C ⊥ (S A H)$

$\Rightarrow S H ⊥ B C \Rightarrow \hat{((S B C), (A B C))} = \hat{S H A} .$

Vậy đáp án C đúng.

+) $(S B C) \cap (S A C) = S C$ nhưng $B C ⊥ S C$ nên đáp án D sai.

Câu 4:

Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?

A. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc $\hat{A I B}$ .

B. $(B C D) ⊥ (A I B) .$

C. Góc giữa hai mặt phẳng (ABC) và (ABD) là góc $\hat{C B D} .$

D. $(A C D) ⊥ (A I B) .$

Xem đáp án

Chọn đáp án C.

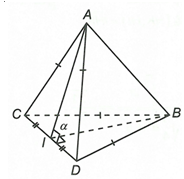
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai? (ảnh 1)

Ta có: $\{\begin{cases} (A B C) \cap (A B D) = A B \\ B C ⊥ A B \\ B D ⊥ A B \end{cases}$

$\Rightarrow \hat{((A B D), (A B C))} \neq \hat{C B D} .$ Đáp án C sai.

Câu 5:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với mặt phẳng (ABCD) và SA = a góc giữa hai mặt phẳng (SAD) và (SBC) bằng

A. 30°.

B. 90°.

C. 0°.

D. 45°.

Xem đáp án

Chọn đáp án D.

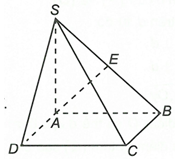
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với mặt phẳng (ABCD) và (ảnh 1)

Ta có $\{\begin{cases} A B ⊥ A D \\ A B ⊥ S A \end{cases} \Rightarrow A B ⊥ (S A D) .$

Gọi E là hình chiếu của A lên SB, dễ thấy $A E ⊥ (S B C) .$

Vậy góc giữa (SAD) và (SBC) là góc giữa AB và AE.

Ta có $∆$ SAB vuông cân tại A nên $\hat{S B A} = 45^{o} .$

Suy ra $\hat{B A E} = 45^{o}$ là góc giữa AB và AE.

Vậy góc giữa hai mặt phẳng (SAD) và (SBC) bằng 45°.

Câu 6:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Côsin của góc hợp bởi hai mặt phẳng (SAB) và (SCD) bằng

A. $\frac{\sqrt{3}}{\sqrt{7}} .$

B. $\frac{2}{\sqrt{7}} .$

C. $\frac{\sqrt{2}}{3} .$

D. $\frac{\sqrt{3}}{2} .$

Xem đáp án

Chọn đáp án A.

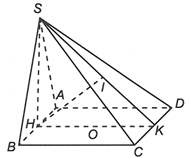
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt (ảnh 1)

Gọi H, K là trung điểm của AB, CD.

Do $(S A B) ⊥ (A B C D)$ nên SH là đường cao của hình chóp.

Ta có $H K ⊥ A B, H K ⊥ S H \Rightarrow H K ⊥ (S A B) (1)$

Dựng $H I ⊥ S K \Rightarrow H I ⊥ (S C D) (2) .$

Từ (1) và (2) ta có góc hợp bởi hai mặt phẳng (SAB) và (SCD) là $(H K, H I) = \hat{I H K} .$

Ta có $S H = \frac{a \sqrt{3}}{2}; H K = a .$

$\frac{1}{H I^{2}} = \frac{1}{S H^{2}} + \frac{1}{H K^{2}} \Rightarrow H I = \frac{\frac{a \sqrt{3}}{2} . a}{\sqrt{\frac{3}{4} a^{2} + a^{2}}} = \frac{\sqrt{21}}{7} .$

Vây $\cos \hat{I H K} = \frac{H I}{H K} = \frac{\sqrt{21}}{7} .$

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a cạnh bên SA vuông góc với đáy và SA = a. Góc giữa hai mặt phẳng (SBC) và (SAD) bằng

A. 30°.

B. 60°.

C. 90°.

D. 45°.

Xem đáp án

Chọn đáp án D.

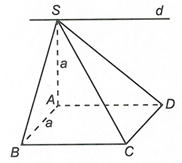
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a cạnh bên SA vuông góc với đáy và SA = a. (ảnh 1)

Mặt phẳng (SBC) và mặt phẳng (SAD) cắt nhau theo giao tuyến là đường thẳng $d / / B C / / A D .$

Vì $S A ⊥ d, S B ⊥ d$ nên $\hat{((S B C), (S A D))} = \hat{(S A, S B)} = \hat{A S B} .$

Vậy $∆$ ASB vuông cân tại A nên $\hat{A S B} = 45^{o} .$

Câu 8:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và

S O = \frac{a \sqrt{3}}{2} .

Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng

A. 30°.

B. 45°.

C. 60°.

D. 90°.

Xem đáp án

Chọn đáp án C.

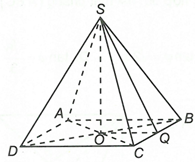
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với (ảnh 1)

Gọi Q là trung điểm BC, suy ra $O Q ⊥ B C .$

Ta có $\{\begin{cases} B C ⊥ O Q \\ B C ⊥ S O \end{cases} \Rightarrow \hat{((S B C), (A B C D))} = \hat{(S Q, O Q)} = \hat{S Q O} .$

Tam giác vuông SOQ có $\tan \hat{S Q O} = \frac{S O}{O Q} = \frac{\frac{a \sqrt{3}}{2}}{\frac{a}{2}} = \sqrt{3} \Rightarrow \hat{S Q O} = 60^{o} .$

Vậy mặt phẳng (SBC) hợp với mặt đáy (ABCD) một góc 60°.

Câu 9:

Cho hình chóp S.ABC có đáy là tam giác vuông tại

B, S A ⊥ (A B C), S A = \sqrt{3} c m, A B = 1 c m .

Mặt bên (SBC) hợp với mặt đáy góc bằng

A. 90°.

B. 60°.

C. 45°.

D. 30°.

Xem đáp án

Chọn đáp án B

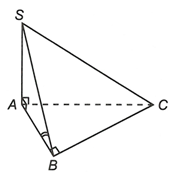
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, SA vuông góc (ABC), SA = căn bậc 2 3 cm, AB = 1cm (ảnh 1)

Ta có $S A ⊥ (A B C)$ nên $S A ⊥ B C$ mà $A B ⊥ B C .$

Suy ra $B C ⊥ (S A B) \Rightarrow S B ⊥ B C .$

$\begin{array}{l} \{\begin{cases} (S B C) \cap (A B C) = B C \\ A B ⊥ B C \\ S B ⊥ B C \end{cases} \Rightarrow \hat{((S B C), (A B C))} = \hat{S B A} . \\ \tan \hat{S B A} = \frac{S A}{A B} = \frac{\sqrt{3}}{1} = \sqrt{3} \Rightarrow \hat{S B A} = 60^{o} . \end{array}$

Vậy góc giữa (SBC) và mặt đáy (ABC) bằng 60^o

Câu 10:

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông, BA = BC = a, cạnh bên

A A^{'} = a \sqrt{2} .

Gọi

φ

là góc hợp bởi hai mặt phẳng (A'BC) và (ABC). Khi đó

A. $\tan φ = \frac{1}{\sqrt{2}} .$

B. $\tan φ = \frac{1}{\sqrt{3}} .$

C. $\tan φ = \sqrt{2} .$

D. $\tan φ = \frac{\sqrt{6}}{3} .$

Xem đáp án

Chọn đáp án C.

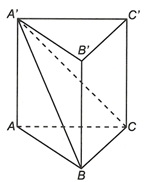
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông, BA = BC = a, cạnh bên AA' = a căn (ảnh 1)

Ta có: $\{\begin{cases} B C ⊥ B A \\ B C ⊥ A A^{'} \end{cases} \Rightarrow B C ⊥ (A A^{'} B^{'} B) \Rightarrow B C ⊥ A^{'} B .$

Do $\{\begin{cases} (A^{'} B C) \cap (A B C) = B C \\ A^{'} B \subset (A^{'} B C); A^{'} B ⊥ B C \\ A B \subset (A B C); A B ⊥ B C \end{cases}$ nên $\hat{A^{'} B A} = φ$ là góc hợp bởi hai mặt phẳng (A'BC) và (ABC).

Xét $∆$ A'BC vuông tại A ta có $\tan φ = \frac{A^{'} A}{B A} = \frac{a \sqrt{2}}{a} = \sqrt{2} .$

Câu 11:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA = a và

S A ⊥ (A B C), A B = B C = a .

Góc giữa hai mặt phẳng (SAC) và (SBC) bằng

A. 45°.

B. 30°.

C. 60°.

D. 90°.

Xem đáp án

Chọn đáp án C.

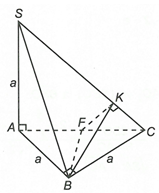
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA = a và SA vuông góc (ABC), AB = BC = a (ảnh 1)

Ta có $(S A C) \cap (S B C) = S C .$

Gọi F là trung điểm AC thì $B F ⊥ (S A C) .$

Dựng $B K ⊥ S C$ tại $K \Rightarrow S C ⊥ (B K F) \Rightarrow \hat{((S A C), (S B C))} = \hat{(K B, K F)} = \hat{B K F} .$

Dễ thấy $Δ C F K ∽ Δ C S A \Rightarrow \frac{F K}{F C} = \frac{S A}{S C} \Rightarrow F K = \frac{F C . S A}{S C} = \frac{\frac{a \sqrt{2}}{2} . a}{a \sqrt{3}} = \frac{a}{\sqrt{6}} .$

$∆$ BFK vuông tại F có $\tan \hat{B K F} = \frac{F B}{F K} = \frac{\frac{a \sqrt{2}}{2}}{\frac{a}{\sqrt{6}}} = \sqrt{3} \Rightarrow \hat{B K F} = 60^{o} .$

Vậy góc giữa hai mặt phẳng (SAC) và (SBC) bằng 60°.

Câu 12:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng

a \sqrt{2}

và SA vuông góc với mặt phẳng (ABCD). Gọi

α

là góc giữa hai mặt phẳng (SBD) và (ABCD). Nếu

\tan α = \sqrt{2}

thì góc giữa (SAC) và (SBC) bằng

A. 30°.

B. 90° .

C. 60°.

D. 45°.

Xem đáp án

Chọn đáp án C.

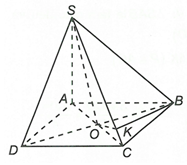
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng a căn bậc 2 2 và (ảnh 1)

Gọi O là tâm đáy và K là hình chiếu vuông góc của O trên SC.

Do $\{\begin{cases} B D ⊥ A C \\ B D ⊥ S A \end{cases}$ nên $B D ⊥ (S A C) \Rightarrow B D ⊥ S O .$

Suy ra góc giữa hai mặt phẳng (SBD) và (ABCD) là góc $\hat{S O A} = α .$

Ta có $\tan α = \frac{S A}{O A} = \sqrt{2} \Rightarrow S A = O A . \sqrt{2} = a .$

Do $\{\begin{cases} S C ⊥ B D \\ S C ⊥ O K \end{cases}$ nên $S C ⊥ B K .$

Suy ra góc giữa hai mặt phẳng (SAC) và (SBC) là $\hat{B K O} .$

Ta có $\tan \hat{B K O} = \frac{B O}{O K} = \frac{B O}{\frac{1}{2} d (A, S C)} = \frac{2 B O}{\frac{S A . A C}{\sqrt{S A^{2} + A C^{2}}}} = \frac{2. \frac{\sqrt{2}}{2} . \sqrt{1^{2} + {\sqrt{2}}^{2}}}{1. \sqrt{2}} = \sqrt{3} .$

Suy ra $\hat{B K O} = 60^{o} .$

Câu 13:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,

∆

SAB là tam giác đều và (SAB) vuông góc với (ABCD). Gọi

φ

là góc tạo bởi (SAC) và (SCD). Giá trị của cos

φ

bằng

A. $\frac{\sqrt{3}}{7} .$

B. $\frac{\sqrt{6}}{7} .$

C. $\frac{5}{7}$ .

D. $\frac{\sqrt{2}}{7} .$

Xem đáp án

Chọn đáp án C.

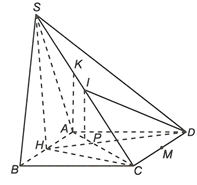
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB là tam giác đều và (SAB) (ảnh 1)

Gọi H, M lần lượt là trung điểm của AB, CD. Vì $∆$ SAB là tam giác đều và (SAB) vuông góc với (ABCD) nên $S H ⊥ (A B C D) .$

Kẻ $A K ⊥ S C (K \in S C), D I ⊥ S C (I \in S C), I P / / A K (P \in A C) .$

Suy ra $φ = \hat{(I P, I D)} .$

Ta có $H C = H D = \frac{a \sqrt{5}}{2}, S C = S D = a \sqrt{2}, S M = \frac{a \sqrt{7}}{2} \Rightarrow D I = \frac{S M . C D}{S D} = \frac{a \sqrt{14}}{4} .$

$\begin{array}{l} Δ C S A = Δ S C D \Rightarrow A K = D I = \frac{a \sqrt{14}}{4} . \\ C I = S K = \sqrt{C D^{2} - D I^{2}} = \frac{a \sqrt{2}}{4} \Rightarrow C K = \frac{3 a \sqrt{2}}{4} . \\ Δ C P I ∽ Δ C A K \Rightarrow I P = \frac{C I}{C K} . A K = \frac{a \sqrt{14}}{12}, A P = \frac{K I}{C K} . A C = \frac{2 a \sqrt{2}}{3} . \end{array}$

Áp dụng định lí côsin, ta có

$∆$ APD có $P D = \sqrt{A P^{2} + A D^{2} - 2 A P . A D . \cos 45^{o}} = \frac{a \sqrt{5}}{3} .$

$∆$ IPD có $\cos \hat{P I D} = \frac{I P^{2} + I D^{2} - D P^{2}}{2. I P . I D} = \frac{5}{7} .$

Vậy $\cos φ = \frac{5}{7} .$

Câu 14:

Cho hình lập phương ABCD.A'B'C'D' cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng AA', BB', CC' thỏa mãn diện tích của tam giác MNP bằng a². Góc giữa hai mặt phẳng (MNP) và (ABCD) là

A. 60°.

B. 30°.

C. 45°.

D. 120°.

Xem đáp án

Chọn đáp án A.

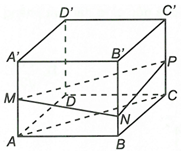
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng AA', BB' (ảnh 1)

Gọi $α$ là số đo góc của hai mặt phẳng (MNP) và (ABCD).

Ta có hình chiếu vuông góc của tam giác MNP lên (ABCD) là $∆$ ABC.

Áp dụng công thức hình chiếu về diện tích ta có

${S^{'}}_{Δ A B C} = S_{Δ M N P} . \cos α \Leftrightarrow \frac{1}{2} A B . B C = a^{2} . \cos α \Rightarrow \cos α = \frac{1}{2} \Rightarrow α = 60^{o} .$

Vậy góc của hai mặt phẳng (MNP) và (ABCD) bằng 60°.

Câu 15:

Cho tam giác ABC vuông cân tại A có AB = a trên đường thẳng d vuông góc với (ABC) tại điểm A ta lấy một điểm D. Góc giữa hai mặt phẳng (ABC) và (DBC) trong trường hợp

∆

DBC là tam giác đều là

A. $\arccos \frac{1}{3} .$

B. $\arccos \frac{\sqrt{3}}{3} .$

C. $\arccos \frac{\sqrt{3}}{4} .$

D. $\arccos \frac{\sqrt{3}}{6} .$

Xem đáp án

Chọn đáp án B.

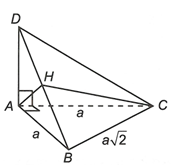
Cho tam giác ABC vuông cân tại A có AB = a trên đường thẳng d vuông góc với (ABC) tại điểm A (ảnh 1)

Gọi $φ$ là góc giữa hai mặt phẳng (ABC) và (DBC).

Theo công thức diện tích hình chiếu của đa giác, ta có: $S_{Δ A B C} = S_{Δ D B C} . \cos φ .$

Mà $S_{Δ D B C} = \frac{1}{2} D B . D C . \sin 60^{o} = \frac{1}{2} a \sqrt{2} . a \sqrt{2} . \frac{\sqrt{3}}{2} = \frac{a^{2} \sqrt{3}}{2} .$

Mặt khác $S_{Δ A B C} = \frac{1}{2} A B . A C = \frac{1}{2} a^{2} .$

Suy ra $\cos φ = \frac{S_{Δ A B C}}{S_{Δ D B C}} = \frac{\sqrt{3}}{3} \Rightarrow φ = \arccos \frac{\sqrt{3}}{3} .$

Câu 16:

Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là một tam giác cân với

A B = A C = a, \hat{B A C} = 120^{o},

cạnh bên BB' = a. Gọi I là trung điểm CC'. Chứng minh rằng tam giác AB'I vuông ở A. Côsin của góc giữa hai mặt phẳng (ABC) và (AB'I) bằng

A. $\frac{\sqrt{15}}{10} .$

B. $\frac{\sqrt{30}}{10} .$

C. $\frac{10}{\sqrt{30}} .$

D. $\frac{\sqrt{15}}{\sqrt{30}} .$

Xem đáp án

Chọn đáp án B.

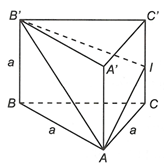
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là một tam giác cân với AB = AC = a. góc BAC = 120 độ, (ảnh 1)

Áp dụng định lý Côsin cho $∆$ ABC ta có:

$B C^{2} = A B^{2} + A C^{2} - 2 A B . A C . \cos A = a^{2} + a^{2} - 2 a^{2} \cos 120^{o} = 3 a^{2} .$

Áp dụng định lý Py-ta-go, ta có:

$B^{'} A^{2} = 2 a^{2}; A I^{2} = a^{2} + {(\frac{a}{2})}^{2} = \frac{5 a^{2}}{4}; B^{'} I^{2} = 3 a^{2} + \frac{a^{2}}{4} = \frac{13 a^{2}}{4} .$

Ta có: $B^{'} A^{2} + A I^{2} = 2 a^{2} + \frac{5 a^{2}}{4} = \frac{13 a^{2}}{4} = B^{'} I^{2} \Rightarrow Δ A B^{'} I$ vuông ở A.

Ta có: $S_{Δ A B^{'} I} = \frac{1}{2} A I . A B^{'} = \frac{1}{2} . \frac{a \sqrt{5}}{2} . a \sqrt{2} = \frac{a^{2} \sqrt{10}}{4} .$

$S_{Δ A B C} = \frac{1}{2} a^{2} \sin 120^{o} = \frac{a^{2} \sqrt{3}}{4} .$

Gọi $φ$ là góc giữa hai mặt phẳng (ABC) và (AB'I).

Ta có $\cos φ = \frac{S_{Δ A B C}}{S_{Δ A B I^{'}}} = \frac{\frac{a^{2} \sqrt{3}}{4}}{\frac{a^{2} \sqrt{10}}{4}} = \frac{\sqrt{3}}{\sqrt{10}} = \frac{\sqrt{30}}{10} .$

Câu 17:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và

S A ⊥ (A B C D),

gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?

A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc $\hat{A B S} .$

B. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc $\hat{S O A} .$

C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc $\hat{S D A} .$

D. $(S A C) ⊥ (S B D) .$

Xem đáp án

Chọn đáp án C

Ta có: $\{\begin{cases} (S A D) \cap (A B C D) = A D \\ A B ⊥ A D, A B \subset (A B C D) \\ S A ⊥ A D, S A \subset (S A D) \end{cases} \Rightarrow \hat{((S A D), (A B C D))} = \hat{S A B} .$

Vậy đáp án C sai.

Câu 18:

Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC), tam giác ABC vuông cân ở A và có đường cao

A H (H \in B C) .

Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?

A. $S A ⊥ (A B C) .$

B. $(S A H) ⊥ (S B C) .$

C. $O \in S C .$

D. Góc giữa (SBC) và (ABC) là $\hat{S B A} .$

Xem đáp án

Chọn đáp án B

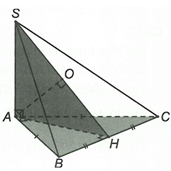
Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC), tam giác ABC vuông (ảnh 1)

Ta có $\{\begin{cases} (S A B) \cap (S A C) = S A \\ (S A C) ⊥ (A B C) \\ (S A B) ⊥ (A B C) \end{cases} \Rightarrow S A ⊥ (A B C) .$

Gọi H là trung điểm của $B C \Rightarrow A H ⊥ B C$ mà $B C ⊥ S A$

$\Rightarrow B C ⊥ (S A H) \Rightarrow (S B C) ⊥ (S A H) .$

Khi đó O là hình chiếu vuông góc của A lên (SBC).

Suy ra

O \in S H

và

\hat{((S B C), (A B C))} = \hat{S H A} \Rightarrow

D sai

Câu 19:

Cho lăng trụ đứng ABC.A'B'C' có diện tích tam giác ABC bằng 5. Gọi M, N, P lần lượt thuộc các cạnh AA', BB', CC' và diện tích tam giác MNP bằng 10. Góc giữa hai mặt phẳng (ABC) và (MNP) bằng

A. 60° .

B. 30° .

C. 90°.

D. 45°.

Xem đáp án

Chọn đáp án A

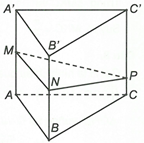
Cho lăng trụ đứng ABC.A'B'C' có diện tích tam giác ABC bằng 5. Gọi M, N, P lần lượt thuộc các (ảnh 1)

Có $∆$ ABC là hình chiếu của MNP lên mặt phẳng (ABC).

Theo công thức diện tích hình chiếu có $S^{'} = S \cos φ$ với

$S^{'} = S_{A B C}; S = S_{M N P}$ và $φ = \hat{((A B C); (M N P))} .$

Suy ra $\cos φ = \frac{S^{'}}{S} = \frac{5}{10} = \frac{1}{2} .$ Suy ra $φ = 60^{o} .$

Câu 20:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và

D; A B = 2 a, A D = D C = a

và

S A ⊥ (A B C D) .

Tan của góc giữa hai mặt phẳng (SBC) và (ABCD) bằng

A. $\frac{1}{\sqrt{2}} .$

B. $\frac{1}{\sqrt{3}} .$

C. $\sqrt{3} .$

D. $\sqrt{2} .$

Xem đáp án

Chọn đáp án A

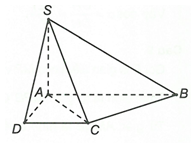
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = 2a, AD = DC = a và SA vuông (ảnh 1)

Ta có $(S B C) \cap (A B C D) = B C .$

Dễ dàng chứng minh được: $A C ⊥ B C .$

$\begin{array}{l} \Rightarrow B C ⊥ (S A C) \Rightarrow B C ⊥ S C \Rightarrow \hat{((S B C), (A B C D))} = \hat{S C A} . \\ \tan \hat{S C A} = \frac{S A}{A C} = \frac{a}{a \sqrt{2}} = \frac{1}{\sqrt{2}} . \end{array}$

Câu 21:

Lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a. Gọi M là điểm trên cạnh AA' sao cho

A M = \frac{3 a}{4} .

Tan của góc hợp bởi hai mặt phẳng (MBC) và (ABC) là

A. 2.

B. $\frac{1}{2}$

C. $\frac{\sqrt{3}}{2} .$

D. $\frac{\sqrt{2}}{2} .$

Xem đáp án

Chọn đáp án C

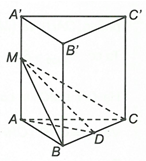
Lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a. Gọi M là điểm trên cạnh AA' sao cho AM = 3a/4 (ảnh 1)

Gọi D là trung điểm của BC.

Ta có $(M B C) \cap (A B C) = B C;$

$B C ⊥ A D; B C ⊥ A M \Rightarrow B C ⊥ (A M D) .$

Do đó $α = \hat{((M B C), (A B C))} = \hat{(D M, A D)} = \hat{M D A} .$

Vì tam giác MAD vuông tại A nên

\tan α = \frac{A M}{A D} = \frac{3 a}{4} . \frac{2}{a \sqrt{3}} = \frac{\sqrt{3}}{2} .

Câu 22:

Cho hình chóp đều S.ABC có chiều cao bằng a, thể tích bằng

\sqrt{3} a^{3} .

Góc tạo bởi mặt bên và mặt đáy bằng

A. 75°.

B. 60°.

C. 45°.

D. 30°.

Xem đáp án

Chọn đáp án C

Gọi M là trung điểm của BC, suy ra $A M ⊥ B C$ (vì $∆$ ABC đều).

Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC, suy ra $S O ⊥ (A B C)$ và SO = a

Khi đó góc giữa mặt bên (SBC) và mặt đáy (ABC) là góc $\hat{S M O} .$

Ta có $V_{S . A B C} = \frac{1}{3} S O . S_{Δ A B C} \Rightarrow S_{Δ A B C} = \frac{3 V_{S . A B C}}{S O} = \frac{3 \sqrt{3} a^{3}}{a} = 3 \sqrt{3} a^{2} .$

Mặt khác $S_{Δ A B C} = \frac{\sqrt{3}}{4} . A B^{2} = 3 \sqrt{3} a^{2} \Rightarrow A B = 2 \sqrt{3} a .$

Xét $∆$ ABC có $O M = \frac{1}{3} A M = \frac{1}{3} . \frac{\sqrt{3}}{2} .2 \sqrt{3} a = a .$

Xét

∆

SOM vuông tại O nên

\tan \hat{S M O} = \frac{S O}{O M} = \frac{a}{a} = 1 \Rightarrow \hat{S M O} = 45^{o} .

Câu 23:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A. Cạnh bên SA vuông góc mặt phẳng đáy và

S A = a \sqrt{2} .

Biết

A B = 2 A D = 2 D C = 2 a .

Góc giữa hai mặt phẳng (SAB) và (SBC) là

A. $\frac{π}{3} .$

B. $\frac{π}{4} .$

C. $\frac{π}{6} .$

D. $\frac{π}{12} .$

Xem đáp án

Chọn đáp án A

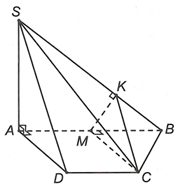
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A. Cạnh bên SA vuông góc mặt phẳng (ảnh 1)

Gọi M là trung điểm của AB.

Ta có tứ giác ADCM là hình vuông và $C M ⊥ (S A B)$ . Trong (SAB) kẻ $M K ⊥ S B$ tại K.

Khi đó, ta có $S B ⊥ (C M K)$ nên $\hat{((S A B); (S B C))} = \hat{M K C} .$

Từ $Δ B M K ∽ Δ B S A$ ta suy ra $M K = \frac{S A . B M}{S B} \Leftrightarrow M K = \frac{1}{\sqrt{3}}$

Trong $∆$ MKC vuông tại M có $\tan \hat{M K C} = \frac{M C}{M K} = \sqrt{3} .$

Suy ra $\hat{M K C} = \frac{π}{3} .$

Câu 24:

Cho hình chóp đều S.ABCD có cạnh đáy bằng

a \sqrt{2},

cạnh bên bằng 2a. Gọi

α

là góc tạo bởi hai mặt phẳng (SAC)và (SCD). Giá trị của cos

α

bằng

A. $\frac{\sqrt{21}}{2} .$

B. $\frac{\sqrt{21}}{14} .$

C. $\frac{\sqrt{21}}{3} .$

D. $\frac{\sqrt{21}}{7} .$

Xem đáp án

Chọn đáp án D

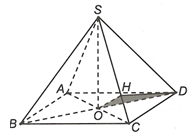
Cho hình chóp đều S.ABCD có cạnh đáy bằng a căn bậc 2 (2) cạnh bên bằng 2a. Gọi alpha là góc (ảnh 1)

Gọi H là hình chiếu của O trên cạnh SC ta có

$\hat{((S D C), (S A C))} = \hat{O H D} = α .$

$∆$ OHD vuông tại O và $O D = a; O H = \frac{a \sqrt{3}}{2}$ nên $D H = \frac{\sqrt{7} a}{2} .$

Vậy $\cos α = \frac{O H}{D H} = \frac{\sqrt{21}}{7} .$

Câu 25:

Cho lăng trụ đứng OAB.O'A'B' có các đáy là các tam giác vuông cân

O A = O B = a, A A^{'} = a \sqrt{2} .

Gọi M, P lần lượt là trung điểm các cạnh OA, AA'. Diện tích thiết diện khi cắt lăng trụ bởi (B'MP) bằng

A. $\frac{a^{2} \sqrt{15}}{12 \sqrt{2}} .$

B. $\frac{5 a^{2} \sqrt{15}}{12 \sqrt{2}} .$

C. $\frac{5 a^{2} \sqrt{15}}{6 \sqrt{2}} .$

D. $\frac{a^{2} \sqrt{15}}{6 \sqrt{2}} .$

Xem đáp án

Chọn đáp án B

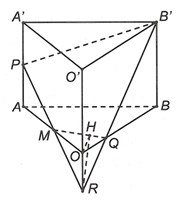
Cho lăng trụ đứng OAB.O'A'B' có các đáy là các tam giác vuông cân OA = OB = a, AA' = a căn bậc 2 2 (ảnh 1)

Gọi R là giao điểm của MP và OO', Q là giao điểm của B'R với OB

Thiết diện là tứ giác MPB'Q, ta có $\frac{O Q}{O^{'} B^{'}} = \frac{R O}{R O^{'}} = \frac{1}{3} \Rightarrow O Q = \frac{a}{3} .$

Tứ giác AMQB là hình chiếu vuông góc của tứ giác PMQB' trên mặt phẳng (OAB) nên $S_{P M Q B^{'}} = \frac{S_{A M Q B}}{\cos φ}$ với $φ$ là góc tạo bởi hai mặt phẳng (OAB) và (MPB'Q).

Ta có: $S_{A M Q B} = S_{O A B} - S_{O M Q} = \frac{1}{2} a^{2} - \frac{1}{12} a^{2} = \frac{5}{12} a^{2} .$

Hạ $O H ⊥ M Q,$ ta có: $\{\begin{cases} M Q ⊥ O H \\ M Q ⊥ O R \end{cases} \Rightarrow M Q ⊥ (O H R) \Rightarrow M Q ⊥ H R .$

Vậy $φ = \hat{O H R}$ ( $\hat{O H R}$ nhọn).

Ta có: $\cos φ = \cos \hat{O H R} = \frac{O H}{R H} = \frac{O H}{\sqrt{O H^{2} + O R^{2}}}$

$= \frac{\frac{a}{\sqrt{13}}}{\sqrt{\frac{a^{2}}{13} + \frac{a^{2}}{2}}} = \frac{\sqrt{2}}{\sqrt{15}} .$

Vậy $S_{P M Q B^{'}} = \frac{5 a^{2} \sqrt{15}}{12 \sqrt{2}} .$

Bài tập chuyên đề Toán 11 Bài 1: Vecto trong không gian - Hai đường thẳng vuông góc có đáp án

Chủ đề 2: Góc Dạng 3. Góc giữa hai mặt phẳng

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương