25 câu hỏi trắc nghiệm thuộc Chủ đề 2: Góc Dạng 2. Góc giữa đường thẳng và mặt phẳng

Câu 1:

Cho tứ diện ABCD có các cạnh BA, BC, BD vuông góc với nhau từng đôi một. Góc giữa đường thẳng CD và mặt phẳng (ADB) là góc

A. $\hat{C D A} .$

B. $\hat{C A B} .$

C. $\hat{B D A} .$

D. $\hat{C D B} .$

Xem đáp án

Chọn đáp án D.

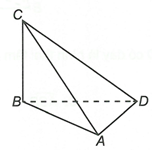
Cho tứ diện ABCD có các cạnh BA, BC, BD vuông góc với nhau từng đôi một. Góc giữa đường (ảnh 1)

Ta có $\{\begin{cases} C B ⊥ B D \\ C B ⊥ B A \end{cases} \Rightarrow C B ⊥ (A B D) .$

Do đó BD là hình chiếu của CD trên (ABD).

Suy ra góc giữa CD và (ABD) bằng $\hat{C D B} .$

Câu 2:

Cho hình chóp S.ABC có SB vuông góc (ABC). Góc giữa SC với (ABC) là góc giữa

A. SC và AC.

B. SC và AB.

C. SC và BC.

D. SC và SB.

Xem đáp án

Chọn đáp án C.

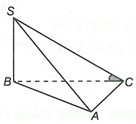
Cho hình chóp S.ABC có SB vuông góc (ABC). Góc giữa SC với (ABC) là góc giữa A. SC và AC. B. SC và AB. (ảnh 1)

Hình chiếu vuông góc của SC lên (ABC) là BC nên góc giữa SC với (ABC) là góc giữa SC và BC.

Câu 3:

Cho hình chóp S.ABCD với ABCD là hình chữ nhật,

S A ⊥ (A B C D) .

Góc giữa SB và (SAD) là góc nào dưới đây?

A. $\hat{B S D} .$

B. $\hat{S B A} .$

C. $\hat{B S A} .$

D. $\hat{S B D} .$

Xem đáp án

Chọn đáp án C.

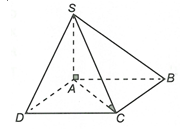
Cho hình chóp S.ABCD với ABCD là hình chữ nhật, SA vuông góc (ABCD). Góc giữa SB và (SAD) là (ảnh 1)

Ta có $S B \cap (S A D) = \{S\} .$

$\begin{array}{l} B A ⊥ S A \\ B A ⊥ A D \end{array}\} \Rightarrow B A ⊥ (S A D)$ tại A

Suy ra SA là hình chiếu của SB lên (SAD)

$\Rightarrow \hat{(S B, (S A D))} = \hat{(S B, S A)} = \hat{B S A} .$

Câu 4:

Cho hình chóp S.ABCD có

S A ⊥ (A B C D)

và đáy là hình thoi tâm O. Góc giữa đường thẳng SB và mặt phẳng (SAC) là góc giữa cặp đường thẳng nào?

A. SB và SA .

B. SB và AB.

C. SB và BC.

D. SB và SO.

Xem đáp án

Chọn đáp án D.

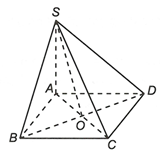
Cho hình chóp S.ABCD có SA vuông góc (ABCD) và đáy là hình thoi tâm O. Góc giữa đường thẳng SB (ảnh 1)

Ta có $B O ⊥ A C, B O ⊥ S A \Rightarrow B O ⊥ (S A C)$

Suy ra hình chiếu của SB lên mặt phẳng (SAC) là SO.

Vậy $\hat{(S B, (S A C))} = \hat{(S B, S O) .}$

Câu 5:

Cho hình chóp S.ABCD có đáy là hình thoi tâm

O, S A ⊥ (A B C D) .

Góc giữa SA và (SBD) là

A. $\hat{A S D} .$

B. $\hat{A S O} .$

C. $\hat{A S B} .$

D. $\hat{S A B} .$

Xem đáp án

Chọn đáp án B.

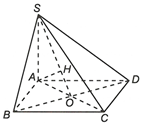
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, SA vuông góc (ABCD). Góc giữa SA và (SBD) là (ảnh 1)

Do $S A ⊥ B D, A C ⊥ B D \Rightarrow B D ⊥ (S A C) .$

Gọi H là hình chiếu của A trên SO.

Khi đó $A H ⊥ S O, A H ⊥ B D .$

Suy ra $A H ⊥ (S B D) .$

Do đó hình chiếu của SA xuống (SBD) là SH.

Vậy góc giữa SA và (SBD) là $\hat{A S H} = \hat{A S O} .$

Câu 6:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA vuông góc mặt đáy và SA = a. Gọi

φ

là góc tạo bởi SB và mặt phẳng (ABCD). Xác định cot

φ

?.

Xem đáp án

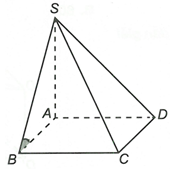
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA vuông góc mặt đáy và SA = a. Gọi (ảnh 1)

Ta có $S B \cap (A B C D) = \{B\} .$

Trên SB chọn điểm S. Ta có $S A ⊥ (A B C D)$ nên A là hình chiếu của S lên (ABCD).

Suy ra $\hat{(S B, (A B C D))} = \hat{(S B, B A)} = \hat{S B A} .$

Vậy $\cot φ = \frac{A B}{S A} = \frac{2 a}{a} = 2.$

Câu 7:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Số đo của góc giữa SA và (ABC).

A. 30°.

B. 45°.

C. 60°.

D. 75°.

Xem đáp án

Chọn đáp án B.

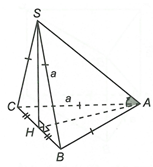
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng (ảnh 1)

Ta có $S H ⊥ (A B C) .$

$\Rightarrow \hat{(S A, (A B C))} = \hat{S A H} = α$

DABC và DSBC là hai tam giác đều cạnh a nên $A H = S H = \frac{a \sqrt{3}}{2} .$

Suy ra $∆$ SHA vuông cân tại $H \Rightarrow α = 45^{o} .$

Câu 8:

Cho hình lập phương ABCD.A'B'C'D'. Góc giữa A'C' và mặt phẳng (BCC'B') bằng

A. 45°.

B. 0°.

C. 90°.

D. 30°.

Xem đáp án

Chọn đáp án A.

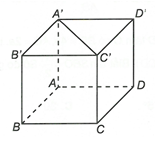
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa A'C' và mặt phẳng (BCC'B') bằng A. 45 độ. B. 0 độ. C. 90 độ. (ảnh 1)

Dễ dàng thấy góc giữa A'C' và mặt phẳng (BCC'B') là $\hat{A^{'} C^{'} B^{'}} = 45^{o} .$

Câu 9:

Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh

a, \hat{A B C} = 60^{o}

và

A A^{'} = a .

Góc hợp bởi đường thẳng BD' và mặt phẳng (ABCD) bằng

A. 90°.

B. 60°.

C. 30°.

D. 45°.

Xem đáp án

Chọn đáp án C.

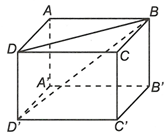
Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, góc ABC = 60 độ và AA' = a. Góc hợp (ảnh 1)

Do $D D^{'} ⊥ (A B C D)$ nên góc hợp bởi đường thẳng BD' và mặt phẳng (ABCD) là $\hat{D^{'} B D} .$

$\tan \hat{D^{'} B D} = \frac{D D^{'}}{B D} = \frac{a}{a \sqrt{3}} = \frac{\sqrt{3}}{3} \Rightarrow \hat{D^{'} B D} = 30^{o} .$

Câu 10:

Cho hình lăng trụ đứng ABC.A'B'C' có

∆

ABC đều cạnh

a, A A^{'} = \sqrt{3} a .

Góc giữa đường thẳng AB' và (ABC) bằng

A. 45°.

B. 30°.

C. 60°.

D. 45°.

Xem đáp án

Chọn đáp án C.

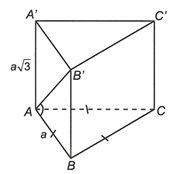
Cho hình lăng trụ đứng ABC.A'B'C' có tam giác ABC đều cạnh a, AA' = căn bậc 2 (3) a. Góc giữa đường (ảnh 1)

ABC.A'B'C' là lăng trụ đứng nên AB là hình chiếu vuông góc của AB' trên (ABC).

Suy ra góc giữa đường thẳng AB' và (ABC) bằng $\hat{B^{'} A B} .$

$∆$ B'AB vuông tại B nên $\tan \hat{B^{'} A B} = \frac{B B^{'}}{A B} = \sqrt{3} \Rightarrow \hat{B^{'} A B} = 60^{o} .$

Câu 11:

Cho hình thoi ABCD tâm O có

B D = 4 a, A C = 2 a .

Lấy điểm S không thuộc (ABCD) sao cho

S O ⊥ (A B C D) .

Biết

\tan \hat{S B O} = \frac{1}{2} .

Số đo góc giữa SC và (ABCD) bằng

A. 60°.

B. 75°.

C. 30°.

D. 45°.

Xem đáp án

Chọn đáp án D.

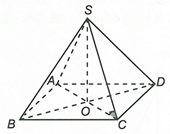
Cho hình thoi ABCD tâm O có BD = 4a, AC = 2a. Lấy điểm S không thuộc (ABCD) sao cho SO vuông góc (ảnh 1)

Góc giữa SC và (ABCD) là góc $\hat{S C O} .$

$\begin{array}{l} B D = 4 a \Rightarrow B O = 2 a; \\ S O = B O . \tan \hat{S B O} = 2 a . \frac{1}{2} = a; \\ A C = 2 a \Rightarrow O C = a . \end{array}$

Vậy $\hat{S C O} = 45^{o} .$

Câu 12:

Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh

a, S A ⊥ (A B C D)

và SA = a. Góc giữa đường thẳng SB và (SAC) là

A. 30°.

B. 75°.

C. 60°.

D. 45°.

Xem đáp án

Chọn đáp án A.

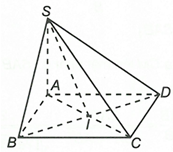
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a, SA vuông góc (ABCD) và SA = a. Góc giữa (ảnh 1)

Gọi I là tâm của hình vuông của ABCD.

Vì ABCD là hình vuông nên $B D ⊥ A C .$

Mặt khác vì $S A ⊥ (A B C D)$ nên $S A ⊥ B D .$

Suy ra $B D ⊥ (S A C)$ do đó góc giữa đường thẳng SB và (SAC) là góc $\hat{B S I} .$

Ta có $S B = a \sqrt{2}; B I = \frac{a \sqrt{2}}{2}$

$\Rightarrow \sin \hat{B S I} = \frac{B I}{S B} = \frac{1}{2} \Rightarrow \hat{B S I} = 30^{o} .$

Câu 13:

Cho khối chóp S.ABC có

S A ⊥ (A B C),

tam giác ABC vuông tại

B, A C = 2 a, B C = a, S B = 2 a \sqrt{3} .

Góc giữa SA và mặt phẳng (SBC) bằng

A. 45°.

B. 30°.

C. 60°.

D. 90°.

Xem đáp án

Chọn đáp án B.

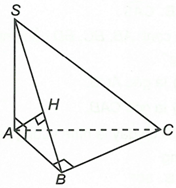
Cho khối chóp S.ABC có SA vuông góc (ABC) tam giác ABC vuông tại B, AC = 2a, BC = a, SB = 2a căn bậc 2(3) (ảnh 1)

Kẻ $A H ⊥ S B (H \in S B) (1) .$

Theo giả thiết, ta có:

$\{\begin{cases} B C ⊥ S A \\ B C ⊥ A B \end{cases} \Rightarrow B C ⊥ (S A B) \Rightarrow B C ⊥ A H (2)$

Từ (1) và (2) suy ra $A H ⊥ (S B C) .$

Do đó góc giữa SA và mặt phẳng (SBC) bằng góc giữa SA và SH bằng $\hat{A S H} .$

Ta có $A B = \sqrt{A C^{2} - B C^{2}} = a \sqrt{3} .$

Trong $∆$ SAB ta có $\sin \hat{A S B} = \frac{A B}{S B} = \frac{a \sqrt{3}}{2 a \sqrt{3}} = \frac{1}{2} .$

Vậy $\hat{A S B} = \hat{A S H} = 30^{o} .$

Do đó góc giữa SA và mặt phẳng (SBC) bằng 30°.

Câu 14:

Cho hình chóp S.ABC có

S A ⊥ (A B C), S A = 2 a \sqrt{3}, A B = 2 a,

tam giác ABC vuông cân tại B. Gọi M là trung điểm của SB. Góc giữa đường thẳng CM và mặt phẳng (SAB) bằng

A. 90°.

B. 60°.

C. 45°.

D. 30°.

Xem đáp án

Chọn đáp án C.

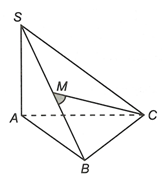
Cho hình chóp S.ABC có SA vuông góc (ABC), SA = 2a căn bậc 2(3), AB = 2a, tam giác ABC vuông cân (ảnh 1)

Ta có: $\{\begin{cases} B C ⊥ A B \\ B C ⊥ S A \end{cases} \Rightarrow B C ⊥ (S A B) .$

Do đó BM là hình chiếu của CM lên mặt phẳng (SAB).

Suy ra $\hat{(C M, (S A B))} = \hat{C M B} .$

Ta có: $\tan \hat{C M B} = \frac{B C}{M B} = \frac{2 A B}{S B} = \frac{2 A B}{\sqrt{S A^{2} + A B^{2}}} = \frac{2.2 a}{\sqrt{{(2 a \sqrt{3})}^{2} + {(2 a)}^{2}}} = 1.$

Suy ra $\hat{C M B} = 45^{o} .$

Vậy $\hat{(C M, (S A B))} = 45^{o} .$

Câu 15:

Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) là

A. $\hat{S C B} .$

B. $\hat{C A S} .$

C. $\hat{S C A} .$

D. $\hat{A S C} .$

Xem đáp án

Chọn đáp án C

Từ giả thiết ta có $S A ⊥ (A B C D)$

Suy ra AC là hình chiếu của SC trên mặt phẳng (ABCD).

Do đó $\hat{(S C, (A B C D))} = \hat{(S C, A C)} = \hat{S C A} .$

Câu 16:

Cho tứ diện ABCB có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?

A. Góc giữa AC và (BCD) là góc ACB.

B. Góc giữa AD và (ABC) là góc ADB.

C. Góc giữa AC và (ABD) là góc CAB.

D. Góc giữa CD và (ABD) là góc CBD.

Xem đáp án

Chọn đáp án A

Từ giả thiết ta có $\{\begin{cases} A B ⊥ B C \\ A B ⊥ C D \end{cases} \Rightarrow A B ⊥ (B C D) .$

Do đó $\hat{(A C, (B C D))} = \hat{(A C, B C)} = \hat{A C B} .$

Câu 17:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,

S A = \sqrt{2} a

và

S A ⊥ (A B C D) .

Góc giữa SC và (ABCD) bằng

A. 45°.

B. 30°.

C. 60°.

D. 90°.

Xem đáp án

Chọn đáp án A

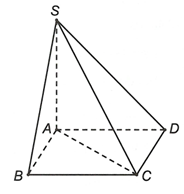
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = căn bậc 2(2) a và SA vuông góc (ABCD). Góc (ảnh 1)

Vì SA vuông góc với đáy nên: $\hat{(S C, (A B C D))} = \hat{(S C, A C)} = \hat{S C A} .$

Trong hình vuông ABCD có $A C = a \sqrt{2} .$

Theo giả thiết, ta có $S A = \sqrt{2} a .$

Suy ra $∆$ SAC vuông cân tại A.

Vậy

\hat{S C A} = 45^{o} .

Câu 18:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2, cạnh bên bằng 3. Số đo của góc giữa cạnh bên và mặt đáy (làm tròn đến phút) gần bằng

A. 69°18'.

B. 28°8'.

C. 75°2'.

D. 61°52'.

Xem đáp án

Chọn đáp án D

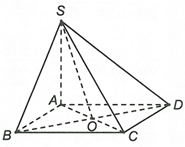
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2, cạnh bên bằng 3. Số đo của góc giữa cạnh (ảnh 1)

Ta có $\hat{(S C, (A B C D))} = \hat{(S C, O C)} = \hat{S C O} .$

Xét tam giác vuông SCO có: $\cos \hat{S C O} = \frac{O C}{S C} = \frac{\sqrt{2}}{3} \Rightarrow \hat{S C O} \approx 61^{o} 52^{'} .$

Câu 19:

Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác đều cạnh a, cạnh bên

A A^{'} = a \sqrt{3} .

Góc giữa đường thẳng AB' và mặt phẳng (ABC) là

A. 45°.

B. 30°.

C. 60°.

D. 90°.

Xem đáp án

Chọn đáp án C

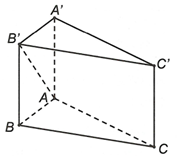
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác đều cạnh a, cạnh bên AA' = a căn bậc 2(3). Góc (ảnh 1)

Vì $B B^{'} ⊥ (A B C)$ nên AB là hình chiếu vuông góc của AB' trên (ABC).

Suy ra $\hat{(A B^{'}, (A B C))} = \hat{(A B^{'}, A B)} = \hat{B^{'} A B} .$

Tam giác ABB' vuông tại B nên: $\tan \hat{B A B^{'}} = \frac{B B^{'}}{A B} = \frac{A A^{'}}{A B} = \sqrt{3} \Rightarrow \hat{B A B^{'}} = 60^{o} .$

Câu 20:

Cho hình chóp đều S.ABC có

S A = 2 a, A B = 3 a .

Góc giữa SA và mặt phẳng (ABC) bằng

A. 30°.

B. 45°.

C. 60°.

D. 90°.

Xem đáp án

Chọn đáp án A

Do hình chóp S.ABC đều nên ta có $S G ⊥ (A B C)$ với G là trọng tâm $∆$ ABC.

Do đó góc giữa SA và mặt phẳng (ABC) là $\hat{S A G} .$

Gọi F là trung điểm của BC ta có $A F = \frac{3 a \sqrt{3}}{2} .$

Suy ra $A G = \frac{2}{3} A F = a \sqrt{3} .$

Xét $∆$ SAG vuông tại G ta có:

$\cos \hat{S A G} = \frac{A G}{S A} = \frac{a \sqrt{3}}{2 a} = \frac{\sqrt{3}}{2} \Rightarrow \hat{S A G} = 30^{o} .$

Vậy góc giữa SA và mặt phẳng (ABC) là 30°.

Câu 21:

Cho hình chóp S.ABCD với đáy ABCD là hình vuông có cạnh a, tâm

O, S A ⊥ (A B C D) .

Góc giữa SC và (SAB) bằng

α

với Góc giữa SO và (ABCD) bằng

A. 90° .

B. 30°.

C. 45°.

D. 60°.

Xem đáp án

Chọn đáp án D

Ta có $\{\begin{cases} B C ⊥ A B \\ B C ⊥ S A \end{cases} \Rightarrow B C ⊥ (S A B)$ nên góc $α$ là $\hat{C S B} .$

Ta có $\tan α = \frac{B C}{S B} = \frac{\sqrt{10}}{5} \Rightarrow S B = \frac{5 a}{\sqrt{10}} \Rightarrow S A = a \sqrt{\frac{3}{2}} .$

Góc giữa SO và (ABCD) là góc $\hat{S O A} .$

Ta có

\tan \hat{S O A} = \frac{S A}{A O} = \frac{a \sqrt{\frac{3}{2}}}{\frac{a \sqrt{2}}{2}} = \sqrt{3} \Rightarrow \hat{S O A} = 60^{o} .

Câu 22:

Cho tứ diện ABCD có ABCD đều cạnh a, AB vuông góc với mặt phẳng (BCD) và AB = 2a. Gọi M là trung điểm của AD. Giá trị tan của góc giữa CM và mặt phẳng (BCD) bằng

A. $\frac{2 \sqrt{3}}{3} .$

B. $2 \sqrt{3} .$

C. $\frac{\sqrt{3}}{2} .$

D. Không xác định.

Xem đáp án

Chọn đáp án A

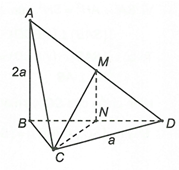
Cho tứ diện ABCD có ABCD đều cạnh a, AB vuông góc với mặt phẳng (BCD) và AB = 2a. Gọi M là (ảnh 1)

Dựng $M N / / A B (N \in B D),$ do $A B ⊥ (B C D)$ và M là trung điểm của AD nên $M N ⊥ (B C D)$ và N là trung điểm của DB.

Suy ra CN là hình chiếu vuông góc của CM trên mặt phẳng (BCD). Vậy góc giữa CM và mặt phẳng (BCD) là góc giữa hai đường thẳng CN và CM.

Ta có: $\tan \hat{(C M, C N)} = \tan \hat{M C N} = \frac{M N}{C N} = \frac{a}{\frac{a \sqrt{3}}{2}} = \frac{2 \sqrt{3}}{3} .$

Câu 23:

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Gọi M là trung điểm của SD. Giá trị tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng

A. $\frac{2}{3}$

B. $\frac{1}{3}$

C. $\frac{1}{2}$

D. $\frac{2}{5} .$

Xem đáp án

Chọn đáp án B

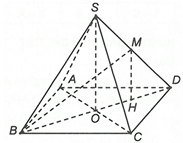
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Gọi M là trung điểm của SD. Giá (ảnh 1)

Gọi $\{O\} = A C \cap B D \Rightarrow S O ⊥ (A B C D) .$

Gọi H là trung điểm của OD.

Xét $∆$ SOD có MH là đường trung bình nên $M H / / S O .$

Suy ra $M H ⊥ (A B C D) .$

Hình chiếu của đường thẳng BM trên mặt phẳng (ABCD) là BH.

Suy ra $\hat{(B M, (A B C D))} = \hat{(B M, B H)} = \hat{M B H}$ ( $\hat{M B H}$ là góc nhọn).

Xét tam giác vuông ABD có:

$B D = \sqrt{A B^{2} + A D^{2}} = \sqrt{{(2 a)}^{2} + {(2 a)}^{2}} = 2 \sqrt{2} a .$

$\Rightarrow B H = \frac{3}{4} B D = \frac{3 \sqrt{2} a}{2}$ và $O D = \frac{1}{2} B D = \sqrt{2} a .$

Xét tam giác vuông SOD có:

$S O = \sqrt{S D^{2} - O D^{2}} = \sqrt{{(2 a)}^{2} - {(\sqrt{2} a)}^{2}} = \sqrt{2} a .$

Suy ra $M H = \frac{1}{2} S O = \frac{\sqrt{2} a}{2} .$ Ta có $\tan \hat{M B H} = \frac{M H}{B H} = \frac{\frac{a \sqrt{2}}{2}}{\frac{3 \sqrt{2} a}{2}} = \frac{1}{3} .$

Câu 24:

Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với mặt đáy; SA = AB = a. Góc giữa SB và mặt phẳng (SAC) bằng

A. 90°.

B. 30°.

C. 45°.

D. 60°.

Xem đáp án

Chọn đáp án B

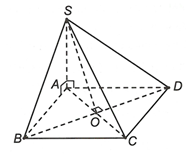
Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với mặt đáy; SA = AB = a. Góc giữa (ảnh 1)

Ta có góc giữa SB và mặt phẳng (SAC) là góc $\hat{B S O} .$

Xét $∆$ SOB vuông tại O có

$S O = \sqrt{S A^{2} + O A^{2}} = \frac{a \sqrt{6}}{2}, S B = \sqrt{S A^{2} + A B^{2}} = a \sqrt{2} .$

Vậy

\cos \hat{B S O} = \frac{S O}{S B} = \frac{\frac{a \sqrt{6}}{2}}{a \sqrt{2}} = \frac{\sqrt{3}}{2} \Rightarrow \hat{B S O} = 30^{o} .

Câu 25:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của

A B, S H = H C, S A = A B .

Gọi

α

là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị tan

α

bằng

A. $\frac{2 \sqrt{3}}{3} .$

B. $\frac{\sqrt{3}}{3} .$

C. $\frac{\sqrt{3}}{2} .$

D. $\frac{1}{\sqrt{2}} .$

Xem đáp án

Chọn đáp án B

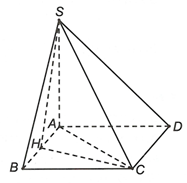
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ảnh 1)

S H = H C = \sqrt{a^{2} + \frac{a^{2}}{4}} = \frac{a \sqrt{5}}{2} .

Vì $S A = A B = a \Rightarrow A H = \frac{a}{2} .$

Vì $S A^{2} + A H^{2} = S H^{2}$ nên $∆$ SAB vuông cân tại A hay $S A ⊥ A B$

Ta có $\{\begin{cases} (S A B) ⊥ (A B C D) \\ (S A B) \cap (A B C D) = A B \\ S A ⊥ A B \end{cases} \Rightarrow S A ⊥ (A B C D) .$

Hình chiếu của SC lên mặt phẳng (ABCD) là AC.

Suy ra $\hat{(S C, (A B C D))} = \hat{(S C, A C)} = \hat{S C A} \Rightarrow \tan α = \tan \hat{S C A} = \frac{S A}{A C} = \frac{a}{a \sqrt{2}} = \frac{1}{\sqrt{2}} .$

Bài tập chuyên đề Toán 11 Bài 1: Vecto trong không gian - Hai đường thẳng vuông góc có đáp án

Chủ đề 2: Góc Dạng 2. Góc giữa đường thẳng và mặt phẳng

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương