Giải Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian
1. Khái niệm mở đầu
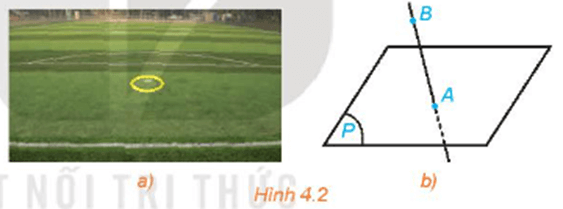
Câu hỏi trang 71 Toán 11 Tập 1: Hãy tìm một số hình ảnh của mặt phẳng trong thực tế.
Lời giải:
Một số hình ảnh của mặt phẳng trong thực tế: mặt bàn, mặt gương phẳng, mặt sàn phẳng, trần nhà phẳng,...
Lời giải:
- Một cục nam châm tròn nhỏ gắn trên mặt bảng cho ta hình ảnh về một điểm thuộc mặt phẳng;
- Một chiếc đầu đinh được gắn vào mặt bàn khi đinh đóng vào bàn cho ta hình ảnh về một điểm thuộc mặt phẳng;
...
2. Các tính chất thừa nhận
Lời giải:
Không thể tìm được đường thẳng nào khác đi qua hai điểm A, B đã cho ngoài đường thẳng tạo bởi xà ngang.
Lời giải:
Cho 3 điểm không thẳng hàng, để tạo được 1 đường thẳng từ 2 trong 3 điểm đó, ta lấy 2 điểm bất kì và xác định đường thẳng đi qua 2 điểm đó. Khi đó số đường thẳng tạo thành là .
a) Đặt khối rubik sao cho ba đỉnh của mặt màu đỏ đều nằm trên mặt bàn. Khi đó, mặt màu đỏ của khối rubik có nằm trên mặt bàn hay không?
b) Có thể đặt khối rubik sao cho 4 đỉnh của nó đều nằm trên mặt bàn hay không?
Lời giải:
a) Khi đặt khối rubik sao cho ba đỉnh của mặt màu đỏ đều nằm trên mặt bàn, mặt màu đỏ của khối rubik nằm trên mặt bàn.
b) Không thể đặt khối rubik sao cho 4 đỉnh của nó đều nằm trên mặt bàn.
Câu hỏi trang 72 Toán 11 Tập 1: Có bao nhiêu mặt phẳng đi qua ba điểm thẳng hàng?
Lời giải:
Qua ba điểm thẳng hàng, ta xác định được duy nhất một đường thẳng. Có vô số mặt phẳng đi qua đường thẳng này nên có vô số mặt phẳng đi qua ba điểm thẳng hàng.
Lời giải:
Vì 4 điểm A, B, C, D tạo thành 1 tứ giác, khi đó 4 điểm A, B, C, D đã đồng phẳng và tạo thành 1 mặt phẳng duy nhất là mặt phẳng (ABCD).
Vậy có 1 mặt phẳng thỏa mãn yêu cầu bài toán.
Lời giải:
Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng. Do đó, khi thiết kế các đồ vật gồm ba chân như chân đỡ máy ảnh, giá treo tranh, kiềng ba chân treo nổi,... ta thấy các đồ vật này có thể đứng thẳng mà không bị đổ trên các bề mặt bởi vì các ba chân của các đồ vật này giống như 3 điểm không thẳng hàng.
Lời giải:
Căng một sợi dây sao cho hai đầu của sợi dây nằm trên mặt bàn. Khi đó, sợi dây nằm trên mặt bàn.
Lời giải:
Đường thẳng AB có hai điểm phân biệt A, B thuộc mặt phẳng (ABC) nên đường thẳng AB nằm trong mặt phẳng (ABC). Vì N thuộc đường thẳng AB nên N thuộc mặt phẳng (ABC).
Theo Ví dụ 2, ta có điểm M thuộc mặt phẳng (ABC). Khi đó đường thẳng MN có hai điểm phân biệt M, N thuộc mặt phẳng (ABC) nên đường thẳng MN nằm trong mặt phẳng (ABC).
Lời giải:
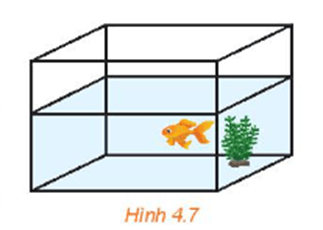
Trong Hình 4.7, mặt nước và thành bể giao nhau theo đường thẳng.
Lời giải:
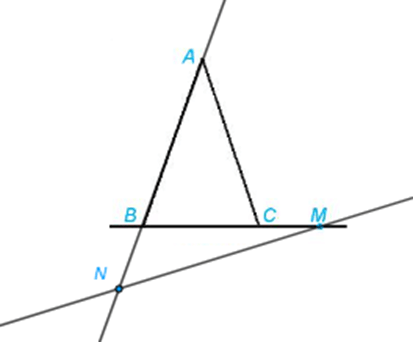
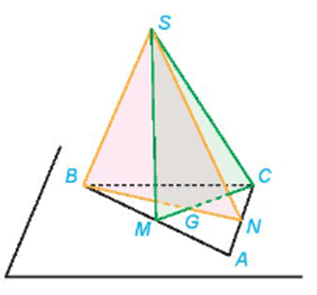
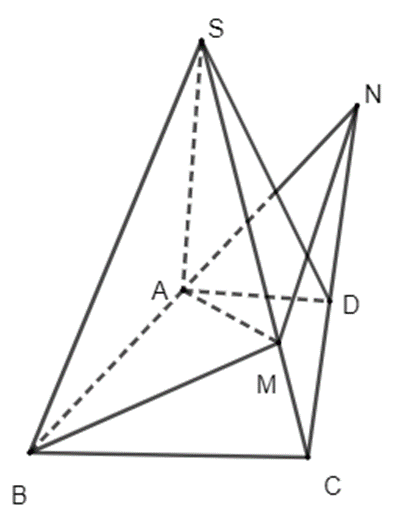
Ta có hai đường thẳng BM và CN cắt nhau tại điểm A.
Do đó, điểm A thuộc đường thẳng BM nên cũng thuộc mặt phẳng (SBM), điểm A thuộc đường thẳng CN nên cũng thuộc mặt phẳng (SCN). Vậy A là một điểm chung của hai mặt phẳng (SBM) và (SCN).
Vì S và A là hai điểm chung của hai mặt phẳng (SBM) và (SCN) nên giao tuyến của hai mặt phẳng này là đường thẳng SA. Ta viết SA = (SBM) ∩ (SCN).
3. Các xác định một mặt phẳng
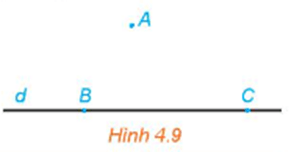
Lời giải:
Đường thẳng d đi qua hai điểm phân biệt B, C thuộc mặt phẳng (ABC) nên đường thẳng d nằm trong mặt phẳng (ABC) hay mặt phẳng (ABC) chứa đường thẳng d. Điểm A thuộc mặt phẳng (ABC) hay mặt phẳng (ABC) chứa điểm A.
Mặt phẳng (ABC) chứa các điểm A, B, C nên mặt phẳng (ABC) chứa hai đường thẳng AB và BC.
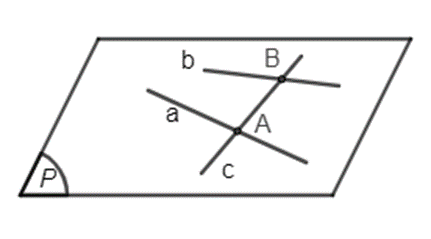
Lời giải:
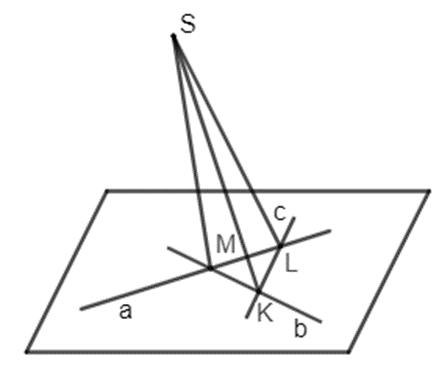
Gọi L là giao điểm của a và c, K là giao điểm của b và c.
Vì L thuộc a nên L thuộc mp(S, a). Vì L thuộc c nên L thuộc mp(S, c). Hai điểm S và L cùng thuộc mp(S, a) và mp(S, c) nên giao tuyến của hai mặt phẳng đó là đường thẳng SL.
Vì K thuộc b nên K thuộc mp(S, b). Vì K thuộc c nên K thuộc mp(S, c). Hai điểm S và K cùng thuộc mp(S, b) và mp(S, c) nên giao tuyến của hai mặt phẳng đó là đường thẳng SK.
Lời giải:
Phụ kiện hít cửa nam châm đại diện cho 1 điểm cố định, một cạnh của cánh cửa đại diện cho một đường thẳng không chứa điểm phụ kiện hít cửa nam châm. Chính vì vậy có một mặt phẳng được xác định khi phụ kiện hít cửa và một cạnh của cánh cửa, khi đó cánh cửa luôn được giữa cố định.
4, Hình chóp và hình tứ diện
Lời giải:
Các hình ảnh đã cho đều có các mặt bên là các tam giác có chung một đỉnh.
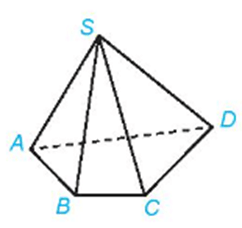
Lời giải:
Hình chóp S.ABCD có
+ Bốn mặt bên là các tam giác SAB, SBC, SCD, SDA.
+ Một mặt đáy là tứ giác ABCD.
Lời giải:
Trong các hình chóp ở HĐ7, hình chóp thứ ba tính từ trái sang (hình khối rubik) có ít mặt nhất.
Hình chóp này có 6 cạnh và 4 mặt.
Lời giải:
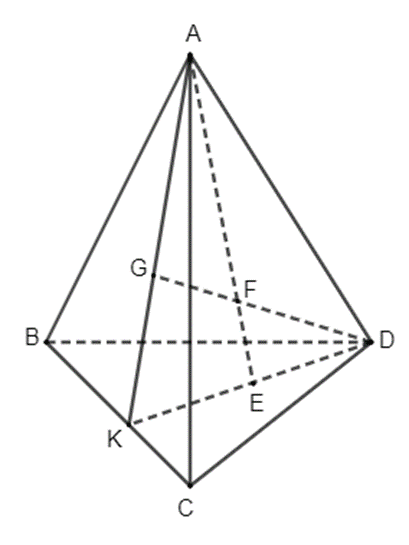
Vì điểm E nằm trong tam giác BCD nên đường thẳng DE cắt cạnh BC tại một điểm K. Các điểm A, E thuộc mặt phẳng (ADK) nên đường thẳng AE thuộc mặt phẳng (ADK), do đó điểm F thuộc mặt phẳng (ADK). Như vậy các điểm A, D, E, F, K cùng thuộc mặt phẳng (ADK).
Trong tam giác ADK, đường thẳng DF cắt AK tại G. Vì G thuộc AK và A, K cùng thuộc mặt phẳng (ABC) nên G thuộc mặt phẳng (ABC). Vậy G là giao điểm của đường thẳng DF và mặt phẳng (ABC).
a) Nếu a chứa một điểm nằm trong (P) thì a nằm trong (P).
b) Nếu a chứa hai điểm phân biệt thuộc (P) thì a nằm trong (P).
c) Nếu a và b cùng nằm trong (P) thì giao điểm (nếu có) của a và b cũng nằm trong (P).
d) Nếu a nằm trong (P) và a cắt b thì b nằm trong (P).
Lời giải:
a) Mệnh đề a) là mệnh đề sai vì đường thẳng a có thể cắt mặt phẳng (P).
b) Mệnh đề b) là mệnh đề đúng (theo tính chất thừa nhận).
c) Mệnh đề c) là mệnh đề đúng.
Giả sử giao điểm của a và b là H, vì H thuộc a và a nằm trong (P) nên H thuộc (P).
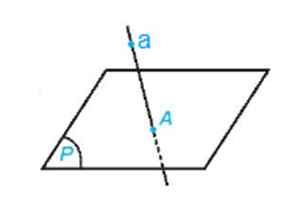
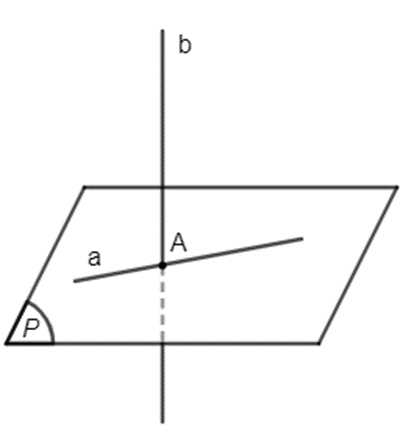
d) Mệnh đề d) là mệnh đề sai.
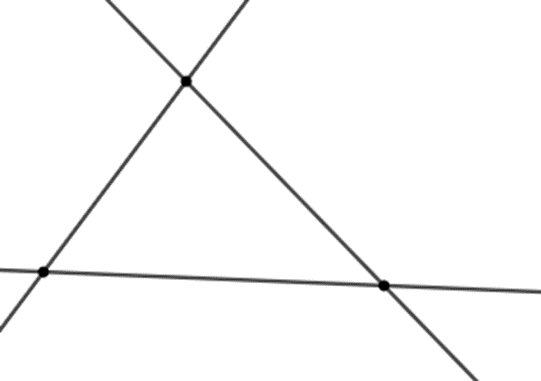
Chẳng hạn trường hợp như trong hình dưới đây có thể xảy ra: đường thẳng b cắt đường thẳng a tại giao điểm A nhưng đường thẳng b không nằm trong mặt phẳng (P).
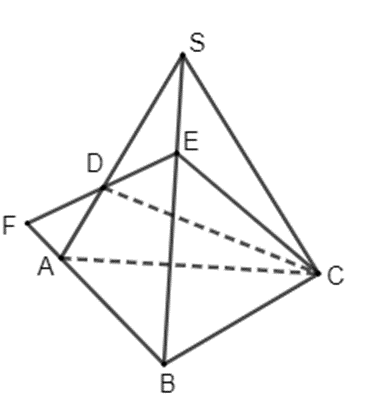
a) Đường thẳng DE có nằm trong mặt phẳng (SAB) không?
b) Giả sử DE cắt AB tại F. Chứng minh rằng F là điểm chung của hai mặt phẳng (SAB) và (CDE).
Lời giải:
a) Vì D thuộc cạnh SA nên D thuộc mặt phẳng (SAB).
Vì E thuộc cạnh SB nên E thuộc mặt phẳng (SAB).
Vì D và E cùng thuộc mặt phẳng (SAB) nên đường thẳng DE nằm trong mặt phẳng (SAB).
b) Vì F thuộc DE nên F thuộc mặt phẳng (CDE).
Vì F thuộc AB nên F thuộc mặt phẳng (SAB).
Do đó, F là điểm chung của hai mặt phẳng (SAB) và (CDE).
Lời giải:
Giả sử đường thẳng c cắt hai đường thẳng a và b lần lượt tại hai điểm phân biệt A và B.
Vì A thuộc a và a nằm trong (P) nên A thuộc (P).
Vì B thuộc B và b nằm trong (P) nên B thuộc (P).
Đường thẳng c có hai điểm phân biệt A và B cùng thuộc mặt phẳng (P) nên tất cả các điểm của đường thẳng c đều thuộc (P) hay đường thẳng c nằm trong mặt phẳng (P).
Lời giải:
Vì N thuộc đường thẳng AB nên N thuộc mặt phẳng (ABM), lại có M thuộc mặt phẳng (ABM) nên đường thẳng MN nằm trong mặt phẳng (ABM) (1).
Vì N thuộc đường thẳng CD nên N thuộc mặt phẳng (SCD), vì M thuộc cạnh SC nên M thuộc mặt phẳng (SCD), do đó đường thẳng MN nằm trong mặt phẳng (SCD) (2).
Từ (1) và (2) suy ra đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD).
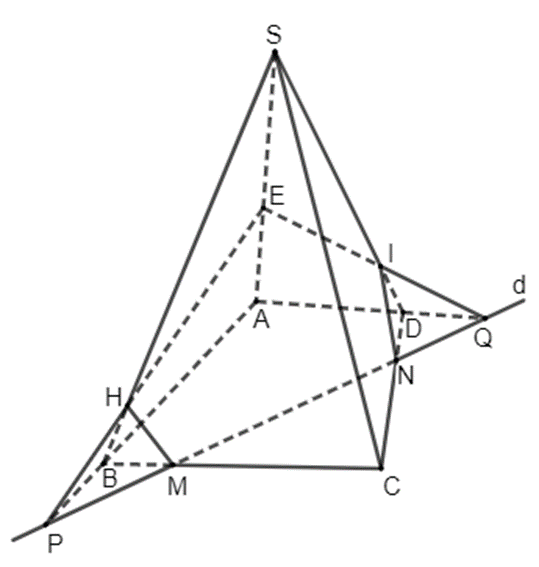
a) Xác định giao điểm của mp(E, d) với các cạnh SB, SD của hình chóp.
b) Xác định giao tuyến của mp(E, d) với các mặt của hình chóp.
Lời giải:
a) +) Vì E thuộc cạnh SA nên E thuộc mặt phẳng (SAB). Vì P thuộc đường thẳng AB nên P thuộc mặt phẳng (SAB). Như vậy, các điểm S, A, B, E, P cùng thuộc mặt phẳng (SAB).
Trong tam giác SAB, đường thẳng EP cắt cạnh SB tại một điểm H. Do P thuộc đường thẳng d nên EP nằm trong mp(E, d) và H thuộc EP, do đó H thuộc mp(E, d). Vậy H là giao điểm của đường thẳng SB và mp(E, d).
+) Vì E thuộc cạnh SA nên E thuộc mặt phẳng (SAD). Vì Q thuộc đường thẳng AD nên Q thuộc mặt phẳng (SAD). Như vậy, các điểm S, A, D, E, Q cùng thuộc mặt phẳng (SAD).
Trong tam giác SAD, đường thẳng EQ cắt cạnh SD tại một điểm I. Do Q thuộc đường thẳng d nên EQ nằm trong mp(E, d) và I thuộc EQ, do đó I thuộc mp(E, d). Vậy I là giao điểm của đường thẳng SD và mp(E, d).
b)
+) Đường thẳng d cắt các cạnh CB, CD lần lượt tại M, N, do đó M, N thuộc d, mà d nằm trong mp(E, d) nên đường thẳng MN cũng nằm trong mp(E, d). Ta lại có, M thuộc CB nằm trong mặt phẳng (ABCD) nên M thuộc mặt phẳng (ABCD), tương tự N thuộc CD nằm trong mặt phẳng (ABCD) nên N thuộc mặt phẳng (ABCD), do đó đường thẳng MN nằm trong mặt phẳng (ABCD). Vậy MN là giao tuyến của hai mặt phẳng (ABCD) và mp(E, d).
+) Vì H thuộc SB nằm trong mặt phẳng (SAB) nên H thuộc mặt phẳng (SAB), lại có E thuộc mặt phẳng (SAB), do đó EH nằm trong mặt phẳng (SAB). Vì E thuộc mp(E, d) và H thuộc mp(E, d) nên EH nằm trong mp(E, d). Vậy EH là giao tuyến của hai mặt phẳng (SAB) và mp(E, d).
+) Vì I thuộc SD nằm trong mặt phẳng (SAD) nên I thuộc mặt phẳng (SAD), lại có E thuộc mặt phẳng (SAD), do đó EI nằm trong mặt phẳng (SAD). Vì E thuộc mp(E, d) và I thuộc mp(E, d) nên EI nằm trong mp(E, d). Vậy EI là giao tuyến của hai mặt phẳng (SAD) và mp(E, d).
+) Vì H thuộc SB nên H thuộc mặt phẳng (SBC), vì M thuộc BC nên M thuộc mặt phẳng (SBC), do đó HM nằm trong mặt phẳng (SBC). Lại có M thuộc d nên M thuộc mp(E, d) và H thuộc mp(E, d) nên HM nằm trong mp(E, d). Vậy HM là giao tuyến của hai mặt phẳng (SBC) và mp(E, d).
+) Vì I thuộc SD nên I thuộc mặt phẳng (SCD), vì N thuộc CD nên N thuộc mặt phẳng (SCD), do đó IN nằm trong mặt phẳng (SCD). Lại có N thuộc d nên N thuộc mp(E, d) và I thuộc mp(E, d) nên IN nằm trong mp(E, d). Vậy IN là giao tuyến của hai mặt phẳng (SCD) và mp(E, d).
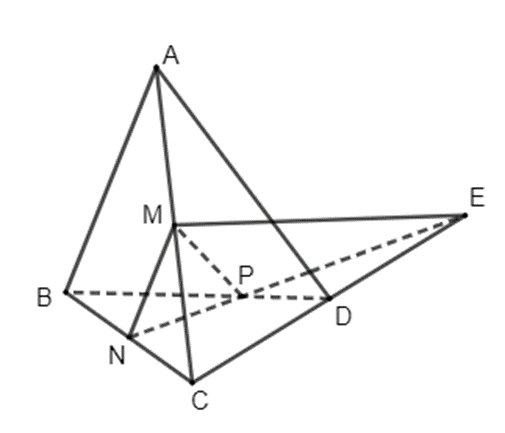
a) Xác định giao điểm của đường thẳng CD và mặt phẳng (MNP).
b) Xác định giao tuyến của hai mặt phẳng (ACD) và (MNP).
Lời giải:
a) Trong tam giác BCD, N thuộc cạnh BC thỏa mãn BN = CN hay N là trung điểm của BC và P thuộc cạnh BD sao cho BP = 2DP. Khi đó, đường thẳng NP cắt CD tại một điểm E. Vì E thuộc NP nằm trong mặt phẳng (MNP) nên E thuộc mặt phẳng (MNP). Vậy E là giao điểm của đường thẳng CD và mặt phẳng (MNP).
b) Vì M thuộc cạnh AC nên M thuộc mặt phẳng (ACD), vì E thuộc CD nên E thuộc mặt phẳng (ACD), do đó đường thẳng ME nằm trong mặt phẳng (ACD).
Vì E thuộc mặt phẳng (MNP) và M thuộc mặt phẳng (MNP) nên ME nằm trong mặt phẳng (MNP).
Vậy ME là giao tuyến của hai mặt phẳng (ACD) và (MNP).
Lời giải:
Ba đầu ngón tay minh họa cho 3 điểm phân biệt không thẳng hàng. Theo tính chất thừa nhận, có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng. Khi đó, mỗi khay, đĩa đồ ăn đại diện cho một mặt phẳng đi qua ba điểm ở đầu ngón tay làm cho khay, đĩa đồ ăn được giữ vững bằng phẳng.
Lời giải:
Phần dao cắt có một đầu được gắn cố định vào bàn, giấy cắt được đặt lên phần bàn hình chữ nhật, khi cắt mặt phẳng cắt giao với mặt phẳng giấy theo một giao tuyến là phần đường cắt nên nó luôn là một đường thẳng.
Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 9: Các số đặc trưng đo xu thế trung tâm
Bài 11: Hai đường thẳng song song
Bài 12: Đường thẳng và mặt phẳng song song
Bài 13: Hai mặt phẳng song song