Giải SGK Toán 10 (Kết nối tri thức) Ước tính số cá thể trong một quần thể

Giải Toán 10 Ước tính số cá thể trong một quần thể

Hoạt động 1 trang 93 Toán 10 Tập 2: Ước tính số hạt lạc trong một hộp

Chuẩn bị:

- Cốc;

- Giấy, bút;

- Một túi lạc.

Tiến hành

Bước 1. Lấy ra một cốc lạc từ trong túi, đếm số lượng và đánh dấu từng hạt lạc.

Bước 2. Đổ lạc đã được đánh dấu vào lại trong túi và xáo trộn đều.

Bước 3. Lấy ra nửa cốc lạc, đếm tổng số hạt lạc và số hạt lạc có đánh dấu trong cốc.

Gọi N là tổng số hạt lạc trong túi ban đầu. Hãy dùng kết quả đếm được ở bước 3 để ước tính N.

Lời giải:

Ta chuẩn bị đầy đủ dụng cụ ở trên và thực hiện theo các bước

Bước 1. Lấy ra một cốc lạc từ trong túi, đếm số lượng và đánh dấu từng hạt lạc.

Chẳng hạn ta đếm được 105 hạt lạc và đánh dấu chúng.

Bước 2. Đổ lạc đã được đánh dấu vào lại trong túi và xáo trộn đều.

Bước 3. Lấy ra nửa cốc lạc, đếm tổng số hạt lạc và số hạt lạc có đánh dấu trong cốc.

Ta đếm được, 54 hạt lạc, trong đó có 9 hạt lạc có đánh dấu.

Gọi N là tổng số hạt lạc trong túi lạc ban đầu. Từ các kết quả ở các bước trên, ta ước tính được N là N ≈ 105 . $\frac{54}{9}$ = 630 (hạt lạc).

Hoạt động 2 trang 94 Toán 10 Tập 2: Đánh giá sai số của ước tính

Trong tiết thực hành trải nghiệm của lớp 10A, tổ của Hà đã thực hiện các bước trên, trong đó lặp lại bước 3 thêm hai lần: lần hai lấy 1 cốc lạc, lần ba lấy 1,5 cốc lạc và thu được kết quả như sau:

Giả sử số hạt lạc trong túi đựng là 1 000 (N = 1 000)  và số hạt lạc được đánh dấu là 100 (M = 100). Kí hiệu $\widehat{N}$ là số quy tròn đến hàng đơn vị của đại lượng M.$\frac{n}{k}$.

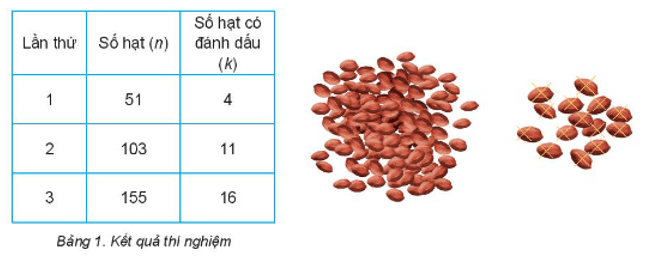
Dựa vào bảng số liệu trong Bảng 1, em hãy hoàn thành bảng tính theo mẫu sau:

Bảng 2. Tính sai số

Em có nhận xét gì về sai số của việc tính xấp xỉ số hạt lạc trong túi khi n càng lớn?

Lời giải:

+ Lần 1: với n = 51, k = 4, ta có: M.$\frac{n}{k}$ = 100.$\frac{51}{4}$ = 1275 => $\widehat{N}$ = 1275

Sai số tuyệt đối ∆_N = |$\widehat{N}$ - N| = |1275 - 1000| = 275.

Sai số tương đối: ${\delta }_N=\frac{{\Delta }_N}{\left|\widehat{N}\right|}=\frac{275}{1275}\approx 21,57\%$

+ Lần 2: với n = 103, k = 11, ta có: M.$\frac{n}{k}$ = 100.$\frac{103}{11}$ ≈ 936 => $\widehat{N}$ = 936

Sai số tuyệt đối ∆_N = |$\widehat{N}$ - N| = |936 - 1000| = 64.

Sai số tương đối: ${\delta }_N=\frac{{\Delta }_N}{\left|\widehat{N}\right|}=\frac{64}{936}\approx 6,84\%$.

+ Lần 2: với n = 155, k = 16, ta có: M.$\frac{n}{k}$ = 100.$\frac{155}{16}$ ≈ 969 => $\widehat{N}$ = 969

Sai số tuyệt đối ∆_N = |$\widehat{N}$ - N| = |969 - 1000| = 31.

Sai số tương đối: ${\delta }_N=\frac{{\Delta }_N}{\left|\widehat{N}\right|}=\frac{31}{969}\approx 3,2\%$.

Vậy ta hoàn thành được bảng đã cho như sau:

Bảng 2. Tính sai số

Nhận xét: Ta thấy sự thay đổi của sai số ước tính khi cỡ mẫu n lớn dần. Khi cỡ mẫu n càng lớn thì sai số của việc tính xấp xỉ số hạt lạc trong túi càng nhỏ.

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 26: Biến cố và định nghĩa cổ điển của xác suất

Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển

Bài tập cuối chương 9 trang 88, 89

Một số nội dung cho hoạt động trải nghiệm hình học

Bài tập ôn tập cuối năm