Đánh giá sai số của ước tính. Trong tiết thực hành trải nghiệm của lớp 10A, tổ của Hà đã thực hiện các bước trên, trong đó lặp lại bước 3 thêm hai lần
Hoạt động 2 trang 94 Toán 10 Tập 2: Đánh giá sai số của ước tính
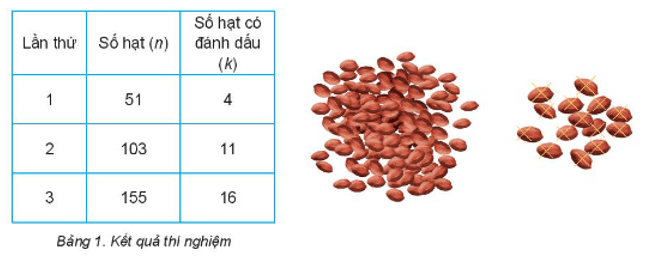
Trong tiết thực hành trải nghiệm của lớp 10A, tổ của Hà đã thực hiện các bước trên, trong đó lặp lại bước 3 thêm hai lần: lần hai lấy 1 cốc lạc, lần ba lấy 1,5 cốc lạc và thu được kết quả như sau:
Giả sử số hạt lạc trong túi đựng là 1 000 (N = 1 000) và số hạt lạc được đánh dấu là 100 (M = 100). Kí hiệu ˆN là số quy tròn đến hàng đơn vị của đại lượng M.nk.
Dựa vào bảng số liệu trong Bảng 1, em hãy hoàn thành bảng tính theo mẫu sau:
|
Lần |
N |
M |
n |
k |
ˆN |
Sai số tuyệt đối |
Sai số tương đối |
|
1 |
1 000 |
100 |
51 |
4 |
? |
? |
? |
|
2 |
1 000 |
100 |
? |
? |
? |
? |
? |
|
3 |
1 000 |
100 |
? |
? |
? |
? |
? |
Bảng 2. Tính sai số
Em có nhận xét gì về sai số của việc tính xấp xỉ số hạt lạc trong túi khi n càng lớn?