Giải SBT Toán 11 (Kết nối tri thức) Bài tập cuối chương 5 trang 87

Giải SBT Toán 11 Bài tập cuối chương 5 trang 87

Trắc nghiệm

Bài 5.26 trang 87 SBT Toán 11 Tập 1: Cho hai dãy số (u_n) và (v_n) thỏa mãn $\underset{n\to +\infty }{\lim }{u}_n=1$ và $\underset{n\to +\infty }{\lim }{v}_n=b\in ℝ$ . Xét các khẳng định sau:

(1) $\underset{n\to +\infty }{\lim }\left(u_n+v_n\right)=1+b$ ;

(2) $\underset{n\to +\infty }{\lim }\frac{v_n}{u_n}=b$ ;

(3) $\underset{n\to +\infty }{\lim }\left(u_n+v_n\right)=b$ ;

(4) $\underset{n\to +\infty }{\lim }\frac{u_n}{v_n}=\frac{1}{b}$ .

Số khẳng định đúng là

A. 2.

B. 1.

C. 3.

D. 4.

Lời giải:

Đáp án đúng là: A

Với $\underset{n\to +\infty }{\lim }{u}_n=1$ và $\underset{n\to +\infty }{\lim }{v}_n=b\in ℝ$ , ta có:

+) $\underset{n\to +\infty }{\lim }\left(u_n+v_n\right)=\underset{n\to +\infty }{\lim }{u}_n+\underset{n\to +\infty }{\lim }{v}_n=1+b$ nên khẳng định (1) đúng, khẳng định (3) sai.

+) $\underset{n\to +\infty }{\lim }\frac{v_n}{u_n}=\frac{\underset{n\to +\infty }{\lim }{v}_n}{\underset{n\to +\infty }{\lim }{u}_n}=\frac{b}{1}=b$ nên khẳng định (2) đúng.

+) Khẳng định (4) đúng khi b ≠ 0.

Vậy có 2 khẳng định đúng.

Bài 5.27 trang 87 SBT Toán 11 Tập 1: Cho $L=\underset{n\to +\infty }{\lim }\left(n^3-2n+1\right)$ . Giá trị của L là

A. L = 0.

B. L = – ∞.

C. L = + ∞.

D. L = 1.

Lời giải:

Đáp án đúng là: C

Ta có $L=\underset{n\to +\infty }{\lim }\left(n^3-2n+1\right)=\underset{n\to +\infty }{\lim }{n}^3\left(1-\frac{2}{n}+\frac{1}{n^3}\right)=+\infty$ .

Bài 5.28 trang 87 SBT Toán 11 Tập 1: Biết $\underset{n\to +\infty }{\lim }\frac{2n^2+n-1}{a{n}^2+1}=1$ với a là tham số. Giá trị của a² – 2a là

A. – 1.

B. 0.

C. 2.

D. Không xác định.

Lời giải:

Đáp án đúng là: B

Ta có $\underset{n\to +\infty }{\lim }\frac{2n^2+n-1}{a{n}^2+1}=\underset{n\to +\infty }{\lim }\frac{2+\frac{1}{n}-\frac{1}{n^2}}{a+\frac{1}{n^2}}=\frac{2}{a}$ .

Mà $\underset{n\to +\infty }{\lim }\frac{2n^2+n-1}{a{n}^2+1}=1$ nên $\frac{2}{a}=1$ , suy ra a = 2.

Do đó, a² – 2a = 2² – 2 . 2 = 0.

Bài 5.29 trang 87 SBT Toán 11 Tập 1: Cho $u_n=\sqrt{n}\left(\sqrt{n+2}-\sqrt{n+1}\right)$ . Khi đó $\underset{n\to +\infty }{\lim }{u}_n$ bằng

A. + ∞.

B. 0.

C. $\frac{1}{2}$ .

D. 1.

Lời giải:

Đáp án đúng là: C

Ta có $\underset{n\to +\infty }{\lim }{u}_n=\underset{n\to +\infty }{\lim }\sqrt{n}\left(\sqrt{n+2}-\sqrt{n+1}\right)$

$=\underset{n\to +\infty }{\lim }\frac{\sqrt{n}\left(n+2-n-1\right)}{\sqrt{n+2}+\sqrt{n-1}}$

$=\underset{n\to +\infty }{\lim }\frac{\sqrt{n}}{\sqrt{n+2}+\sqrt{n+1}}$

$=\underset{n\to +\infty }{\lim }\frac{1}{\sqrt{1+\frac{2}{n}}+\sqrt{1+\frac{1}{n}}}=\frac{1}{2}$ .

Bài 5.30 trang 87 SBT Toán 11 Tập 1: Tính tổng $S=-\frac{2}{3}+\frac{2}{9}-\frac{2}{27}+\mathrm{...}+{\left(-1\right)}^n\frac{2}{3^n}+\mathrm{...}$

A. $S=\frac{1}{2}$ .

B. $S=-\frac{1}{2}$ .

C. S = – 3.

D. S = 3.

Lời giải:

Đáp án đúng là: B

Nhận thấy tổng $S=-\frac{2}{3}+\frac{2}{9}-\frac{2}{27}+\mathrm{...}+{\left(-1\right)}^n\frac{2}{3^n}+\mathrm{...}$ là tổng của cấp số nhân lùi vô hạn với số hạng đầu $u_1=-\frac{2}{3}$ và công bội $q=-\frac{1}{3}$ .

Do đó, $S=\frac{u_1}{1-q}=\frac{-\frac{2}{3}}{1-\left(-\frac{1}{3}\right)}=-\frac{1}{2}$ .

Bài 5.31 trang 87 SBT Toán 11 Tập 1: Cho hàm số f(x) thỏa mãn $\underset{x\to 1^{+}}{\lim }f\left(x\right)=3$ và $\underset{x\to 1^{-}}{\lim }f\left(x\right)=-3$ . Khẳng định đúng là

A. $\underset{x\to 1}{\lim }f\left(x\right)=3$ .

B. $\underset{x\to 1}{\lim }f\left(x\right)=0$ .

C. Không tồn tại $\underset{x\to 1}{\lim }f\left(x\right)$ .

D. $\underset{x\to 1}{\lim }f\left(x\right)=-3$ .

Lời giải:

Đáp án đúng là: C

Do $\underset{x\to 1^{+}}{\lim }f\left(x\right)=3$ và $\underset{x\to 1^{-}}{\lim }f\left(x\right)=-3$ nên $\underset{x\to 1^{+}}{\lim }f\left(x\right)\ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$ .

Vậy không tồn tại $\underset{x\to 1}{\lim }f\left(x\right)$ .

Bài 5.32 trang 88 SBT Toán 11 Tập 1: Cho hàm số f(x) thỏa mãn $\underset{x\to 1^{+}}{\lim }f\left(x\right)=2$ và $\underset{x\to 1^{-}}{\lim }f\left(x\right)=m+1$ . Biết giới hạn của f(x) khi x → 1 tồn tại. Giá trị của m là

A. m = 1.

B. m = – 1.

C. m = 3.

D. Không tồn tại m.

Lời giải:

Đáp án đúng là: A

Ta có giới hạn của f(x) khi x → 1 tồn tại khi và chỉ khi $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }f\left(x\right)$ .

Điều đó có nghĩa là 2 = m + 1, suy ra m = 1.

Bài 5.33 trang 88 SBT Toán 11 Tập 1: Biết hàm số $f\left(x\right)=\left(\begin{array}{c}{x}^2+a neu x\le 1\\ 2x+b neu x>1\end{array}\right)$ có giới hạn khi x → 1. Giá trị của a – b bằng

A. – 1.

B. 0.

C. 1.

D. 3.

Lời giải:

Đáp án đúng là: C

Ta có $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(2x+b\right)=2.1+b=2+b$ ;

$\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(x+a\right)=1+a$.

Vì hàm số $f\left(x\right)=\left(\begin{array}{c}{x}^2+a neu x\le 1\\ 2x+b neu x>1\end{array}\right)$ có giới hạn khi x → 1 nên $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }f\left(x\right)$ , tức là 2 + b = 1 + a, từ đó suy ra a – b = 1.

Bài 5.34 trang 88 SBT Toán 11 Tập 1: Giới hạn $\underset{x\to 1^{+}}{\lim }\frac{x-1}{\sqrt{x-1}}$ là

A. + ∞.

B. Không tồn tại.

C. 2.

D. 0.

Lời giải:

Đáp án đúng là: D

Vì x → 1⁺ nên x > 1, suy ra x – 1 > 0, do đó $\sqrt{x-1}$ có nghĩa.

Ta có $\underset{x\to 1^{+}}{\lim }\frac{x-1}{\sqrt{x-1}}=\underset{x\to 1^{+}}{\lim }\frac{{\left(\sqrt{x-1}\right)}^2}{\sqrt{x-1}}=\underset{x\to 1^{+}}{\lim }\sqrt{x-1}=\sqrt{1-1}=0$ .

Bài 5.35 trang 88 SBT Toán 11 Tập 1: Cho $f\left(x\right)=\frac{x^2-x}{\left(x\right)}$ . Khi đó, giới hạn $\underset{x\to 0}{\lim }f\left(x\right)$ là

A. 0.

B. – 1.

C. 1.

D. Không tồn tại.

Lời giải:

Đáp án đúng là: D

Ta có $\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\frac{x^2-x}{\left(x\right)}=\underset{x\to 0^{-}}{\lim }\frac{x^2-x}{-x}=\underset{x\to 0^{-}}{\lim }\left(-x+1\right)=-0+1=1$ ;

$\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }\frac{x^2-x}{\left(x\right)}=\underset{x\to 0^{+}}{\lim }\frac{x^2-x}{x}=\underset{x\to 0^{+}}{\lim }\left(x-1\right)=0-1=-1$.

Suy ra $\underset{x\to 0^{-}}{\lim }f\left(x\right)\ne \underset{x\to 0^{+}}{\lim }f\left(x\right)$ .

Vậy không tồn tại giới hạn $\underset{x\to 0}{\lim }f\left(x\right)$ .

Bài 5.36 trang 88 SBT Toán 11 Tập 1: Giới hạn $\underset{x\to -\infty }{\lim }\frac{\sqrt{x^2+2}-x}{x}$ là

A. + ∞.

B. 0.

C. – 2.

D. Không tồn tại.

Lời giải:

Đáp án đúng là: C

Ta có $\underset{x\to -\infty }{\lim }\frac{\sqrt{x^2+2}-x}{x}=\underset{x\to -\infty }{\lim }\frac{\left(x\right)\sqrt{1+\frac{2}{x^2}}-x}{x}$

$=\underset{x\to -\infty }{\lim }\frac{-x\sqrt{1+\frac{2}{x^2}}-x}{x}=\underset{x\to -\infty }{\lim }\left(-\sqrt{1+\frac{2}{x^2}}-1\right)=-2$.

Bài 5.37 trang 88 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\left(\begin{array}{c}2 neu -1<x\le 1\\ 1-x neu x\le -1 hoac x>1\end{array}\right)$ . Mệnh đề đúng là

A. Hàm số f(x) liên tục trên [– 1; 1].

B. Hàm số f(x) liên tục trên (– 1; 1].

C. Hàm số f(x) liên tục trên [– 1; 1).

D. Hàm số f(x) liên tục trên ℝ.

Lời giải:

Đáp án đúng là: C

+ Với x < – 1 thì f(x) = 1 – x là hàm đa thức nên nó liên tục trên (– ∞; – 1).

+ Với – 1 < x < 1 thì f(x) = 2 luôn liên tục trên (– 1; 1).

+ Với x > 1 thì f(x) = 1 – x luôn liên tục trên (1; + ∞).

Do đó, hàm số đã cho liên tục trên các khoảng (– ∞; – 1); (– 1; 1) và (1; + ∞).

+ Xét tại điểm x = – 1, ta có f(– 1) = 1 – (– 1) = 2;

$\underset{x\to -1^{-}}{\lim }f\left(x\right)=\underset{x\to -1^{-}}{\lim }\left(1-x\right)=1-\left(-1\right)=2$; $\underset{x\to -1^{+}}{\lim }f\left(x\right)=\underset{x\to -1^{+}}{\lim }2=2$ .

Do đó, $\underset{x\to -1^{-}}{\lim }f\left(x\right)=\underset{x\to -1^{+}}{\lim }f\left(x\right)=f\left(-1\right)$ nên hàm số đã cho liên tục tại x = – 1.

+ Xét tại điểm x = 1, ta có f(1) = 2;

$\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }2=2$; $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(1-x\right)=1-1=0$ .

Do đó, $\underset{x\to 1^{-}}{\lim }f\left(x\right)\ne \underset{x\to 1^{+}}{\lim }f\left(x\right)$ nên hàm số đã cho không liên tục tại x = 1.

Vậy hàm số f(x) liên tục trên [– 1; 1) là mệnh đề đúng.

Bài 5.38 trang 88 SBT Toán 11 Tập 1: Xét hàm số $f\left(x\right)=\left(\begin{array}{c}\frac{x^2+3x+2}{x+1} neu x\ne -1\\ m neu x=-1\end{array}\right)$ với m là tham số. Hàm số f(x) liên tục trên ℝ khi

A. m = 0.

B. m = 3.

C. m = – 1.

D. m = 1.

Lời giải:

Đáp án đúng là: D

Với x ≠ – 1 thì $f\left(x\right)=\frac{x^2+3x+2}{x+1}$ là hàm phân thức nên nó liên tục trên ℝ \{– 1}.

Vậy hàm số f(x) liên tục trên ℝ khi nó liên tục tại x = – 1.

Ta có $\underset{x\to -1}{\lim }f\left(x\right)=\underset{x\to -1}{\lim }\frac{x^2+3x+2}{x+1}=\underset{x\to -1}{\lim }\frac{\left(x+2\right)\left(x+1\right)}{x+1}=\underset{x\to -1}{\lim }\left(x+2\right)=-1+2=1$ .

Hàm số đã cho liên tục tại x = – 1 khi và chỉ khi $\underset{x\to -1}{\lim }f\left(x\right)=f\left(-1\right)$ $\iff m=1$ .

Bài 5.39 trang 89 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{x\left(x-1\right)}{\sqrt{x-1}}$ . Hàm số này liên tục trên

A. (1; + ∞).

B. (– ∞; 1).

C. [1; + ∞).

D. (– ∞; 1].

Lời giải:

Đáp án đúng là: A

Biểu thức $\frac{x\left(x-1\right)}{\sqrt{x-1}}$ xác định khi x – 1 > 0, tức là x > 1.

Do đó, hàm số $f\left(x\right)=\frac{x\left(x-1\right)}{\sqrt{x-1}}$ có tập xác định là (1; + ∞).

Vậy hàm số này liên tục trên (1; + ∞).

Bài 5.40 trang 89 SBT Toán 11 Tập 1: Cho phương trình x⁷ + x⁵ = 1. Mệnh đề đúng là

A. Phương trình có nghiệm âm.

B. Phương trình có nghiệm trong khoảng (0; 1).

C. Phương trình có nghiệm trong khoảng (1; 2).

D. Phương trình vô nghiệm.

Lời giải:

Đáp án đúng là: B

Xét hàm số f(x) = x⁷ + x⁵ – 1.

Đây là hàm đa thức nên nó liên tục trên ℝ.

Do đó, hàm số f(x) liên tục trên đoạn [0; 1] và [1; 2].

Ta có f(0) = 0⁷ + 0⁵ – 1 = – 1 < 0; f(1) = 1⁷ + 1⁵ – 1 = 1 > 0 và f(2) = 2⁷ + 2⁵ – 1 > 0.

Suy ra f(0) . f(1) < 0.

Do vậy tồn tại ít nhất một điểm c ∈ (0; 1) sao cho f(c) = 0.

Từ đó suy ra f(x) = 0 hay phương trình x⁷ + x⁵ = 1 có nghiệm trong khoảng (0; 1).

Tự luận

Bài 5.41 trang 89 SBT Toán 11 Tập 1: Cho dãy số (u_n) thỏa mãn |u_n| ≤ 1. Tính $\underset{n\to +\infty }{\lim }\frac{u_n}{n+1}$ .

Lời giải:

Đặt $v_n=\frac{u_n}{n+1}$ , ta có $\left(v_n\right)=\left(\frac{u_n}{n+1}\right)\le \frac{1}{n+1}$ .

Mà $\frac{1}{n+1}\to 0$ khi n → + ∞.

Khi đó $\underset{n\to +\infty }{\lim }{v}_n=0$ . Vậy $\underset{n\to +\infty }{\lim }\frac{u_n}{n+1}=0$ .

Bài 5.42 trang 89 SBT Toán 11 Tập 1: Tìm giới hạn của dãy số (u_n) với $u_n=\frac{n\sqrt{1+2+\mathrm{...}+n}}{2n^2+3}$ .

Lời giải:

Vì 1, 2, ..., n là một cấp số cộng gồm n số hạng với u₁ = 1 và công sai d = 1.

Do đó 1 + 2 + ... + n = $\frac{n\left(n+1\right)}{2}$ .

Ta có $u_n=\frac{n\sqrt{1+2+\mathrm{...}+n}}{2n^2+3}$$=\frac{n\sqrt{\frac{n\left(n+1\right)}{2}}}{2n^2+3}=\frac{n\sqrt{n\left(n+1\right)}}{\sqrt{2}\left(2n^2+3\right)}$ .

Vậy $\underset{n\to +\infty }{\lim }{u}_n=\underset{n\to +\infty }{\lim }\frac{n\sqrt{n\left(n+1\right)}}{\sqrt{2}\left(2n^2+3\right)}=\underset{n\to +\infty }{\lim }\frac{\sqrt{1+\frac{1}{n}}}{\sqrt{2}\left(2+\frac{3}{n^2}\right)}=\frac{1}{2\sqrt{2}}$ .

Bài 5.43 trang 89 SBT Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:

a) − 0,(31);

b) 2,(121).

Lời giải:

a) Ta có − 0,(31) = – (0,31 + 0,0031 + ... + 0,00...31 + ...)

$=-\left(\frac{31}{100}+\frac{31}{{100}^2}+\mathrm{...}+\frac{31}{{100}^n}+\mathrm{...}\right)$

$=-\frac{\frac{31}{100}}{1-\frac{1}{100}}=-\frac{31}{99}$ .

b) Ta có 2,(121) = 2 + 0,121 + 0,000121 + ... + 0,000...121 + ...

$=2+\frac{121}{1000}+\frac{121}{{1000}^2}+\mathrm{...}+\frac{121}{{1000}^n}+\mathrm{...}$

$=2+\frac{\frac{121}{1000}}{1-\frac{1}{1000}}=2+\frac{121}{999}=\frac{2119}{999}$ .

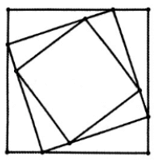
Bài 5.44 trang 89 SBT Toán 11 Tập 1: Cho hình vuông H₁ có cạnh bằng a. Chia mỗi cạnh của hình vuông này thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông H₂. Lặp lại cách làm như trên với hình vuông H₂ để được hình vuông H₃. Tiếp tục quá trình trên ta nhận được dãy hình vuông H₁, H₂, H₃, ..., H_n, ... Gọi s_n là diện tích của hình vuông H_n.

a) Tính s_n.

b) Tính tổng T = s₁ + s₂ + ... + s_n + ...

Lời giải:

a) Áp dụng định lí Pythagore, ta có cạnh của hình vuông H₂ là

$a_2=\sqrt{{\left(\frac{a}{4}\right)}^2+{\left(\frac{3a}{4}\right)}^2}=a\sqrt{\frac{5}{8}}$.

Khi đó diện tích của hình vuông H₂ là $s_2={\left(a\sqrt{\frac{5}{8}}\right)}^2=\frac{5}{8}{a}^2$ .

Mà diện tích của hình vuông H₁ là s₁ = a².

Do đó, $s_2=\frac{5}{8}{a}^2=\frac{5}{8}{s}_1$ .

Lí luận tương tự, ta có $s_3=\frac{5}{8}{s}_2,\mathrm{....,}{s}_n=\frac{5}{8}{s}_{n-1}={\left(\frac{5}{8}\right)}^{n-1}{a}^2$ .

b) Ta có T = s₁ + s₂ + ... + s_n + ... $=a^2\left(1+\frac{5}{8}+{\left(\frac{5}{8}\right)}^2+\mathrm{...}+{\left(\frac{5}{8}\right)}^{n-1}+\mathrm{...}\right)$ .

Vì $\mathrm{1,}\frac{5}{8},{\left(\frac{5}{8}\right)}^2\mathrm{,...,}{\left(\frac{5}{8}\right)}^{n-1}\mathrm{,...}$ là cấp số nhân lùi vô hạn với u₁ = 1 và công bội q = $\frac{5}{8}$ nên

$1+\frac{5}{8}+{\left(\frac{5}{8}\right)}^2+\mathrm{...}+{\left(\frac{5}{8}\right)}^{n-1}+\mathrm{...}=\frac{1}{1-\frac{5}{8}}=\frac{8}{3}$.

Vậy $T=\frac{8a^2}{3}$ .

Bài 5.45 trang 89 SBT Toán 11 Tập 1: Tìm a là số thực thỏa mãn $\underset{x\to +\infty }{\lim }\left(\frac{2x^2+1}{x^2+2x+3}+a^2+3a\right)=0$ .

Lời giải:

Ta có $\underset{x\to +\infty }{\lim }\left(\frac{2x^2+1}{x^2+2x+3}+a^2+3a\right)=\underset{x\to +\infty }{\lim }\left(\frac{2+\frac{1}{x^2}}{1+\frac{2}{x}+\frac{3}{x^2}}+a^2+3a\right)$ = 2 + a² + 3a.

Để $\underset{x\to +\infty }{\lim }\left(\frac{2x^2+1}{x^2+2x+3}+a^2+3a\right)=0$ thì 2 + a² + 3a = 0.

Giải phương trình bậc hai a² + 3a + 2 = 0 ta được a = – 1 và a = – 2.

Vậy a ∈ {– 1; – 2} thì thỏa mãn yêu cầu bài toán.

Bài 5.46 trang 89 SBT Toán 11 Tập 1: Tính các giới hạn sau:

a) $\underset{x\to -\infty }{\lim }\frac{x\left(x+1\right)\left(2x-1\right)}{5x^3+x+7}$ ;

b) $\underset{x\to -\infty }{\lim }\left(x^3-1\right)\left(2-x^5\right)$ ;

c) $\underset{x\to +\infty }{\lim }\left(\sqrt[3]{x^3+x^2+1}-x\right)$ .

Lời giải:

a)$\underset{x\to -\infty }{\lim }\frac{x\left(x+1\right)\left(2x-1\right)}{5x^3+x+7}=\underset{x\to -\infty }{\lim }\frac{x^3\left(1+\frac{1}{x}\right)\left(2-\frac{1}{x}\right)}{x^3\left(5+\frac{1}{x^2}+\frac{7}{x^3}\right)}$

$=\underset{x\to -\infty }{\lim }\frac{\left(1+\frac{1}{x}\right)\left(2-\frac{1}{x}\right)}{5+\frac{1}{x^2}+\frac{7}{x^3}}=\frac{2}{5}$.

b)$\underset{x\to -\infty }{\lim }\left(x^3-1\right)\left(2-x^5\right)=\underset{x\to -\infty }{\lim }{x}^3\left(1-\frac{1}{x^3}\right)x^5\left(\frac{2}{x^5}-1\right)$

$=\underset{x\to -\infty }{\lim }{x}^8\left(1-\frac{1}{x^3}\right)\left(\frac{2}{x^5}-1\right)=-\infty$.

c)$\underset{x\to +\infty }{\lim }\left(\sqrt[3]{x^3+x^2+1}-x\right)$

$=\underset{x\to +\infty }{\lim }\frac{x^3+x^2+1-x^3}{\sqrt[3]{{\left(x^3+x^2+1\right)}^2}+x\sqrt[3]{x^3+x^2+1}+x^2}$

$=\underset{x\to +\infty }{\lim }\frac{x^2+1}{\sqrt[3]{{\left(x^3+x^2+1\right)}^2}+x\sqrt[3]{x^3+x^2+1}+x^2}$

$=\underset{x\to +\infty }{\lim }\frac{1+\frac{1}{x^2}}{\sqrt[3]{{\left(1+\frac{1}{x}+\frac{1}{x^3}\right)}^2}+\sqrt[3]{1+\frac{1}{x}+\frac{1}{x^3}}+1}=\frac{1}{3}$

Bài 5.47 trang 90 SBT Toán 11 Tập 1: Tính $\underset{x\to -\infty }{\lim }\left(1-x\right)\left(1-2x\right)\mathrm{...}\left(1-2018x\right)$ .

Lời giải:

Ta có $\underset{x\to -\infty }{\lim }\left(1-x\right)\left(1-2x\right)\mathrm{...}\left(1-2018x\right)$

$=\underset{x\to -\infty }{\lim }{x}^{2018}\left(\frac{1}{x}-1\right)\left(\frac{1}{x}-2\right)\mathrm{...}\left(\frac{1}{x}-2018\right)=+\infty$.

Bài 5.48 trang 90 SBT Toán 11 Tập 1: Biết $\underset{x\to 0}{\lim }\frac{\sin x}{x}=1$ . Hãy tính:

a) $\underset{x\to 0}{\lim }\frac{\sin x}{x^3}$ ;

b) $\underset{x\to 0^{+}}{\lim }\frac{\sin x}{x^2}$ ;

c) $\underset{x\to 0^{-}}{\lim }\frac{\sin x}{x^2}$ .

Lời giải:

a) $\underset{x\to 0}{\lim }\frac{\sin x}{x^3}=\underset{x\to 0}{\lim }\left(\frac{\sin x}{x}.\frac{1}{x^2}\right)=\underset{x\to 0}{\lim }\frac{\frac{\sin x}{x}}{x^2}$ .

Vì $\underset{x\to 0}{\lim }\frac{\sin x}{x}=1$ > 0; $\underset{x\to 0}{\lim }{x}^2=0$ và x² > 0 nên $\underset{x\to 0}{\lim }\frac{\sin x}{x^3}=+\infty$ .

b) $\underset{x\to 0^{+}}{\lim }\frac{\sin x}{x^2}=\underset{x\to 0^{+}}{\lim }\frac{\frac{\sin x}{x}}{x}$ .

Vì $\underset{x\to 0}{\lim }\frac{\sin x}{x}=1$ nên $\underset{x\to 0^{+}}{\lim }\frac{\sin x}{x}=1>0$ ; và x > 0 nên $\underset{x\to 0^{+}}{\lim }\frac{\sin x}{x^2}=+\infty$ .

c) $\underset{x\to 0^{-}}{\lim }\frac{\sin x}{x^2}=\underset{x\to 0^{-}}{\lim }\frac{\frac{\sin x}{x}}{x}$ .

Vì $\underset{x\to 0}{\lim }\frac{\sin x}{x}=1$ nên $\underset{x\to 0^{-}}{\lim }\frac{\sin x}{x}=1>0$ ; $\underset{x\to 0-}{\lim }x=0$ và x < 0 nên $\underset{x\to 0^{-}}{\lim }\frac{\sin x}{x^2}=-\infty$ .

Bài 5.49 trang 90 SBT Toán 11 Tập 1: Tính $\underset{x\to 0}{\lim }x\sin \frac{1}{x}$ .

Lời giải:

Đặt $f\left(x\right)=x\sin \frac{1}{x}$ . Lấy dãy số (x_n) bất kì thỏa mãn x_n → 0. Khi đó

$\left(f\left(x_n\right)\right)=\left(x_n\right).\left(\sin \frac{1}{x_n}\right)\le \left(x_n\right)\to 0$.

Do đó $\underset{n\to +\infty }{\lim }f\left(x_n\right)=0$ .

Vậy $\underset{x\to 0}{\lim }x\sin \frac{1}{x}=0$ .

Bài 5.50 trang 90 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{\sqrt{x-1}-\sqrt{1-x}}{x}$ . Phải bổ sung thêm giá trị f(0) bằng bao nhiêu để hàm số f(x) liên tục tại x = 0?

Lời giải:

Biểu thức $\frac{\sqrt{x-1}-\sqrt{1-x}}{x}$ có nghĩa khi $\left(\begin{array}{c}x-1\ge 0\\ 1-x\ge 0\\ x\ne 0\end{array}\right)\iff \left(\begin{array}{c}x\ge 1\\ x\le 1\\ x\ne 0\end{array}\right)\iff x=1$ .

Do đó, tập xác định của hàm số $f\left(x\right)=\frac{\sqrt{x-1}-\sqrt{1-x}}{x}$ là D = {1}.

Mà x = 0 không thuộc tập xác định của hàm số nên hàm số đã cho không liên tục tại x = 0.

Vậy không có giá trị của f(0) thỏa mãn.

Bài 5.51 trang 90 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\left(\begin{array}{c}\frac{1}{x} neu x\ne 0\\ 2 neu x=0\end{array}\right)$ .

a) Chứng minh rằng f(– 1) ∙ f(1) < 0.

b) Chứng minh rằng phương trình f(x) = 0 không có nghiệm thuộc khoảng (– 1; 1).

c) Có kết luận gì về tính liên tục của hàm số f(x) trên đoạn [– 1; 1]?

Lời giải:

a) Ta có $f\left(-1\right)=\frac{1}{-1}=-1$ ; $f\left(1\right)=\frac{1}{1}=1$ .

Do đó, f(– 1) ∙ f(1) = (– 1) . (1) = – 1 < 0.

b) Ta thấy f(0) = 2 và $f\left(x\right)=\frac{1}{x}\ne 0\forall x\in \left(-1;1\right)\backslash \left(0\right)$nên phương trình f(x) = 0 không có nghiệm thuộc khoảng (– 1; 1).

c) Ta có $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }\frac{1}{x}=+\infty$và $\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\frac{1}{x}=-\infty$.

Suy ra $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)$. Nên hàm số đã cho không liên tục tại x = 0.

Vậy hàm số f(x) không liên tục trên đoạn [– 1; 1].

Bài 5.52 trang 90 SBT Toán 11 Tập 1: Một điểm dịch vụ trông giữ xe ô tô thu phí 30 nghìn đồng trong giờ đầu tiên và thu thêm 20 nghìn đồng cho mỗi giờ tiếp theo

a) Viết hàm số f(x) mô tả số tiền phí theo thời gian trông giữ.

b) Xét tính liên tục của hàm số này.

Lời giải:

a) Theo bài ra ta có hàm số f(x) mô tả số tiền phí theo thời gian trông giữ là

$f\left(x\right)=\left(\begin{array}{c}30khi0<x\le 1\\ 30+20\left(x-1\right)khix>1\end{array}\right)=\left(\begin{array}{c}30khi0<x\le 1\\ 10+20xkhix>1\end{array}\right)$.

b)

+ Với 0 < x < 1 thì f(x) = 30 luôn liên tục trên (0; 1).

+ Với x > 1 thì f(x) = 10 + 20x là hàm đa thức nên nó luôn liên tục trên (1; +∞).

Ta xét tại điểm x = 1, ta có:

f(1) = 30; $\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }30=30$ và $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(10+20x\right)=10+20.1=30$.

Suy ra $f\left(1\right)=\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }f\left(x\right)$nên hàm số f(x) liên tục tại x = 1.

Vậy hàm số f(x) liên tục trên khoảng (0; + ∞).

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 14: Phép chiếu song song

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục