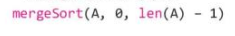Giải Chuyên đề Tin học 11 Bài 9: Sắp xếp trộn
Liệu kĩ thuật chia để trị có thể áp dụng cho bài toán sắp xếp được không? Nếu có thì có làm tăng hiệu quả của sắp xếp được không?
Lời giải:
Kỹ thuật chia để trị có thể được áp dụng cho bài toán sắp xếp, và thực tế nó đã được sử dụng để thiết kế các thuật toán sắp xếp hiệu quả như QuickSort và MergeSort.
Tuy nhiên, trong thực tế, cách tiếp cận này không phải lúc nào cũng làm tăng hiệu quả của thuật toán sắp xếp. QuickSort và MergeSort, mặc dù sử dụng phương pháp chia để trị, thường là những thuật toán có hiệu quả cao. Nhưng nếu áp dụng phương pháp chia để trị cho một thuật toán sắp xếp khác như BubbleSort hoặc InsertionSort, chẳng hạn, thì không có nhiều lợi ích. Trong những trường hợp đó, việc sử dụng phương pháp chia để trị có thể làm giảm hiệu quả của thuật toán sắp xếp.
1. Ý tưởng thuật toán sắp xếp trộn
Hình 9.1. Mô phỏng sắp xếp trộn
Lời giải:
Đặc thù của 3 giai đoạn là: Chia nhỏ dãy gốc thành các dãy với kích thước nhỏ hơn (bằng dãy ban đầu), tiếp tục cho đến khi nhận được các dãy con đã sắp xếp đúng thì tiến hành trộn các dãy này để nhận được kết quả cuối cùng.
Lời giải:
Để trộn hai dãy số B và C, ta có thể sử dụng phương pháp trộn hai mảng đã được sắp xếp.
Ý tưởng của phương pháp này là tạo ra một mảng mới D có độ dài bằng tổng độ dài của hai mảng B và C, và sau đó lần lượt chọn phần tử nhỏ nhất trong hai mảng B và C để đưa vào mảng D cho đến khi hai mảng B và C đều đã được chọn hết và thu được mảng D gồm các số sắp xếp theo thứ tự tăng dần như sau: D = 1, 2, 3, 4, 6, 7
Lời giải:
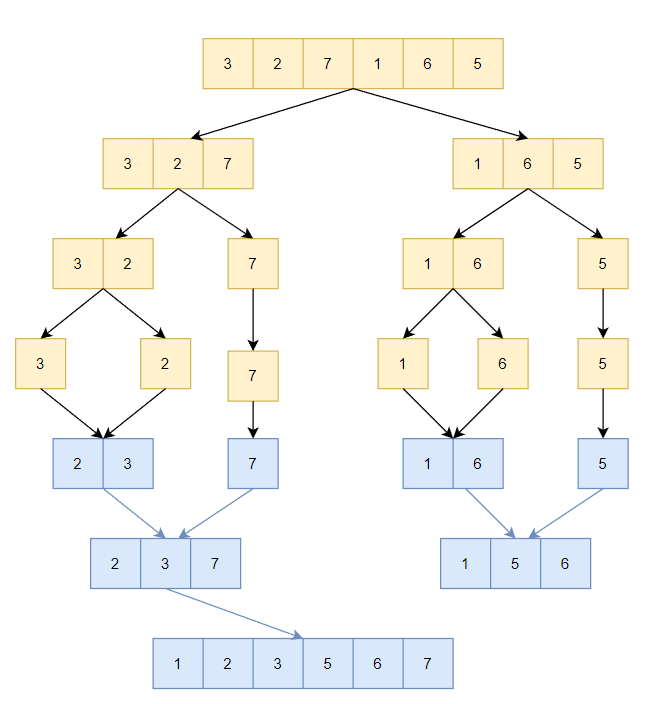
2. Mô tả thuật toán sắp xếp trộn
Lời giải:
- Các bước sắp xếp trộn (merge sort) như sau:
1. Nếu mảng chỉ có một phần tử hoặc không có phần tử nào, thì mảng đó đã được sắp xếp và ta không cần phải làm gì thêm.
2. Chia mảng thành hai phần bằng cách tìm chỉ số giữa (midpoint).
3. Đệ quy sắp xếp phần đầu tiên của mảng (từ đầu đến giữa).
4. Đệ quy sắp xếp phần thứ hai của mảng (từ giữa đến cuối).
5. Trộn (merge) hai phần đã được sắp xếp thành một mảng mới. Khi trộn, ta so sánh phần tử đầu tiên của từng mảng và chọn phần tử nhỏ hơn để đưa vào mảng mới. Sau đó, ta lặp lại quá trình này cho đến khi hết phần tử trong một trong hai mảng. Cuối cùng, ta đưa tất cả các phần tử còn lại của mảng còn lại vào mảng mới.
6. Trả về mảng đã được sắp xếp.
Các bước này sẽ được lặp lại cho đến khi tất cả các phần tử của mảng đã được sắp xếp.
- Cài đặt:
Lời giải:
Ta biết rằng i ban đầu bằng 0 và tăng lên 1 sau mỗi lần lặp, do đó i sẽ tăng từ 0 đến m-1 (tổng cộng m bước lặp).
Tương tự, j ban đầu bằng 0 và tăng lên 1 sau mỗi lần lặp, nên j sẽ tăng từ 0 đến n-1 (tổng cộng n bước lặp).
Vì vậy, số bước lặp tối đa của vòng lặp này là min(m, n) (tức là số phần tử ít hơn trong hai dãy B và C). Do đó, vòng lặp sẽ lặp tối đa min(m, n) lần
Lời giải:
Mô tả các bước thực hiện chương trình 2 nếu dãy gốc A chỉ có một phần tử:
Nếu dãy có 1 phần tử thì trả về kết quả là dãy A ngay.
3. Đánh giá thuật toán sắp xếp trộn
Lời giải:
Gọi T(n) là thời gian chạy của thuật toán sắp xếp trộn.
Với n = 1, dòng lệnh 2 trả lại ngay dãy gốc A, do đó T(1) = 1.
Trường hợp tổng quát
- Tại bước chia (dòng 5), cần O(1) thời gian để thực hiện.
- Các dòng 6, 7 sẽ mất 2T(n/2) thời gian.
- Dòng lệnh 8 thực hiện trộn hai dãy với thời gian O(n).
Tổng kết lại chúng ta các công thức sau tính thời gian T(n).
T(1)=1
T(n) = 2T(n/2) + O(n), n > 1 (1)
Không mất tổng quát, giả sử tồn tại hằng số C > 0 sao cho:
T(n) = 2T (n/2)+ Cn, n > 1 (2)
Các công thức (1), (2) được gọi là công thức truy hồi để tính độ phức tạp thời gian T(n)
của thuật toán trộn.
Người ta tính được: T(n) = O(nlogn).
Lời giải:
Thời gian chạy của thuật toán sắp xếp trộn nếu A = [3, 1] →n = 2:
T(2) = O(2log2) ≈ 2× 0.3 = 0.6
Lời giải:
Mô tả thực hiện các bước của sắp xếp trộn với dãy A = [5, 1, 7, 4]
T(4) = O(4log4) ≈ 2× 0.6 = 1.2
Luyện tập
Luyện tập 1 trang 44 Chuyên đề Tin học 11: Viết chương trình thực hiện công việc sau:
- Dữ liệu được nhập từ tệp văn bản Data.inp bao gồm hai dòng, mỗi dòng là một dãy các số nguyên đã được sắp xếp theo thứ tự tăng dần, các số cách nhau bởi dấu cách. Hai dãy này có thể không bằng nhau về kích thước.
- Chương trình sẽ thực hiện trộn hai dãy trên và đưa kết quả dãy được trộn ra tệp Data.out theo một hàng ngang.
Lời giải:
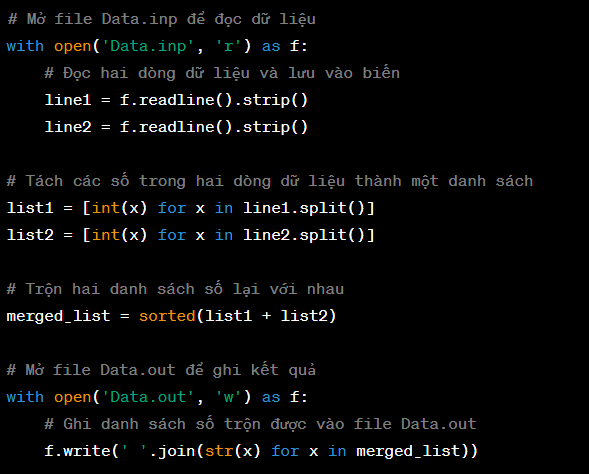
Đây là một ví dụ về cách viết chương trình bằng ngôn ngữ Python để trộn hai dãy số được lưu trữ trong tệp văn bản "Data.inp" và ghi kết quả vào tệp "Data.out":
- Đầu tiên, chương trình sử dụng hàm open() để mở tệp "Data.inp" với chế độ đọc dữ liệu (‘r’).
- Sau đó, chương trình đọc hai dòng dữ liệu từ tệp bằng cách sử dụng phương thức readline(), và loại bỏ các ký tự trắng ở đầu và cuối dòng bằng phương thức strip().
- Tiếp theo, chương trình sử dụng phương thức split() để tách các số trong hai dòng dữ liệu thành một danh sách các số nguyên. Hàm int() được sử dụng để chuyển đổi các chuỗi số sang kiểu số nguyên.
- Sau đó, chương trình trộn hai danh sách số lại với nhau bằng cách sử dụng phương thức sorted() để sắp xếp danh sách theo thứ tự tăng dần.
- Cuối cùng, chương trình sử dụng hàm open() để mở tệp "Data.out" với chế độ ghi dữ liệu ('w'), và sử dụng phương thức write() để ghi danh sách số trộn được vào tệp. Hàm join() được sử dụng để chuyển đổi các số trong danh sách trở lại thành chuỗi, và ký tự dấu cách được sử dụng để ngăn cách giữa các số.
Lời giải:
Chương trình hoàn chỉnh như sau:
Vận dụng
Lời giải:
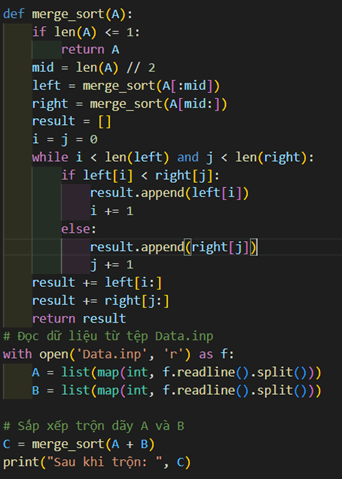
Chương trình hoàn chỉnh như sau:
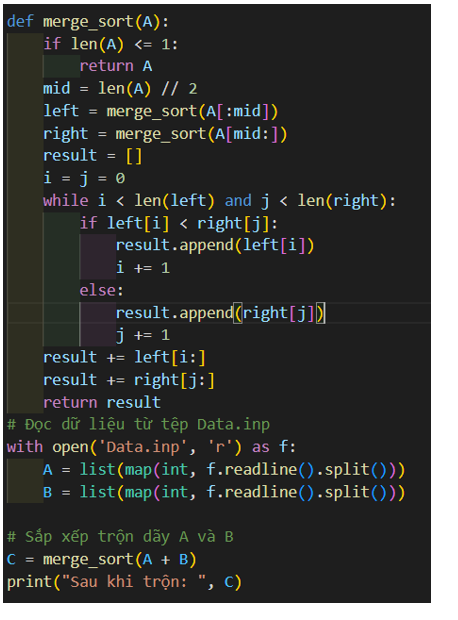
- Thủ tục trộn sẽ có dạng sau: merge(A,left,mid,right). Thủ tục này sẽ trộn hai phân đoạn của dãy A là A[left], ...., A[mid] và A[mid + 1]..... A[right]. Hai phân đoạn này phải được sắp xếp đúng trước đó.
- Thuật toán chính có dạng mergeSoft(A, left, right) như sau:
- Lệnh gọi hàm đệ quy là:
Lời giải:
1. Đầu tiên, ta cần import các thư viện time và random để thực hiện đo thời gian và sinh số ngẫu nhiên cho dãy số:
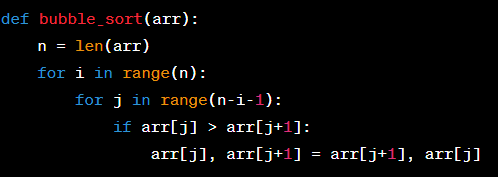
2. Tiếp theo, ta sẽ tạo một hàm để sắp xếp dãy số bằng thuật toán sắp xếp nổi bọt:
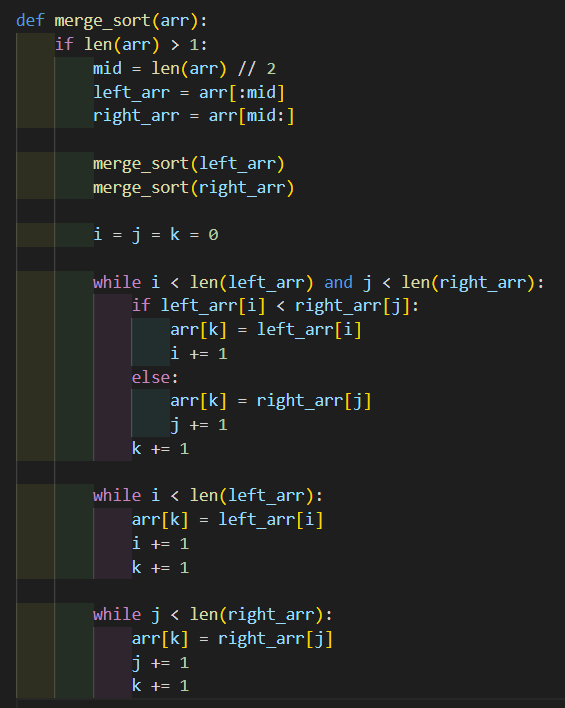
3. Sau đó, ta cần tạo một hàm để sắp xếp dãy số bằng thuật toán sắp xếp trộn:
4. Tiếp theo, ta sẽ đọc dãy số từ tệp văn bản và lưu vào một list:
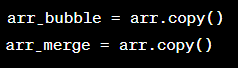
5. Tiếp theo, ta tạo một bản sao của list này để thực hiện sắp xếp bằng hai cách khác nhau:
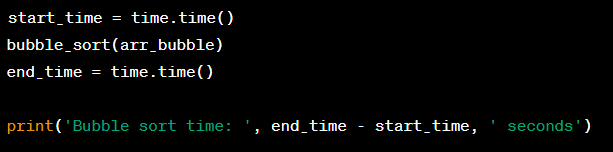
6. Sau đó, ta thực hiện sắp xếp bằng thuật toán sắp xếp nổi bọt và đo thời gian chạy:
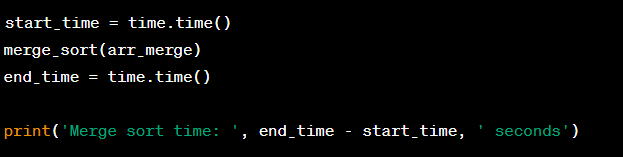
7. Tiếp theo, ta thực hiện sắp xếp bằng thuật toán sắp xếp trộn và đo thời gian chạy:
8. In kết quả mảng sau khi sắp xếp:
Xem thêm lời giải bài tập Chuyên đề học tập Tin học lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 7: Thiết kế thuật toán theo kĩ thuật chia để trị
Bài 8: Thực hành thiết thuật toán tìm kiếm theo kĩ thuật chia để trị
Bài 10: Thực hành giải toán bằng kĩ thuật chia để trị


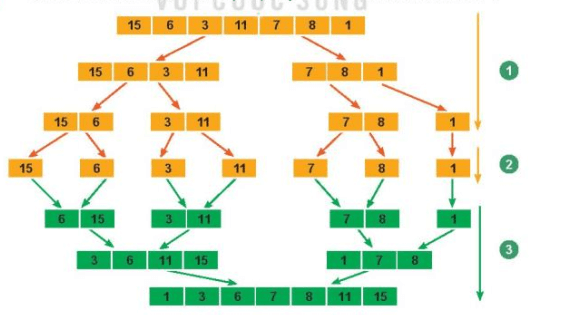


![Mô tả thực hiện các bước của sắp xếp trộn với dãy A = [5, 1, 7, 4]](https://vietjack.com/chuyen-de-tin-hoc-11/images/cau-hoi-2-trang-44-chuyen-de-tin-hoc-11-khmt-kntt-187327.PNG)