Giải Chuyên đề Tin học 11 Bài 8: Thực hành thiết thuật toán tìm kiếm theo kĩ thuật chia để trị
Hình 1. Máy tính ENIAC
Lời giải:
Bài tập này có thể dễ dàng giải bằng phương pháp tìm kiếm tuần tự đã biết. Gọi count là số lần xuất hiện của C trong dãy. Thực hiện tìm kiếm tuần tự với C, mỗi lần tìm thấy C, tăng biến count lên 1.

Luyện tập
Ví dụ nếu A = [0, 1, 2, 2, 2, 2, 4, 5, 5, 6], C = 2, thì kết quả trả lại là 2, 5, 4.
Lời giải:
Trả lời:
- Chương trình trả về ba giá trị start, end và count, tương ứng với chỉ số đầu tiên, chỉ số cuối cùng và số lượng phần tử của vùng có giá trị bằng C trong dãy A.
- Trong trường hợp không tìm thấy C trong dãy A, chương trình trả về -1, -1, 0.
- Nếu giá trị tại vị trí mid bằng C, ta sử dụng hai biến start và end để tìm ra chỉ số đầu tiên và cuối cùng của vùng có giá trị bằng C. Sau đó, ta trả về giá trị start + 1, end - 1 và end - start - 1.
- Nếu giá trị tại vị trí mid nhỏ hơn C, ta tiếp tục tìm kiếm phần tử có giá trị bằng C ở nửa bên phải của dãy A.
- Nếu giá trị tại vị trí mid lớn hơn C, ta tiếp tục tìm kiếm phần tử có giá trị bằng C ở nửa bên trái của dãy A.
Ví dụ chạy thử chương trình:
Thu được kết quả:
Vận dụng
Lời giải:
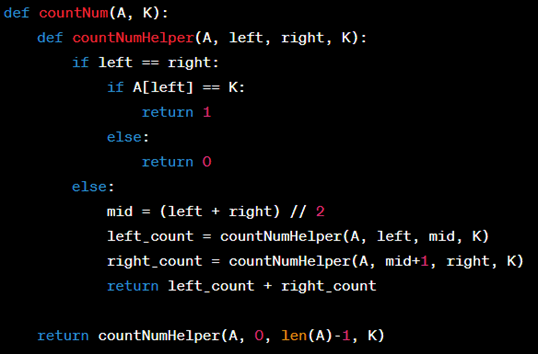
Để tìm số lần xuất hiện của K trong một dãy số chưa được sắp xếp bằng phương pháp chia để trị, ta có thể sử dụng đệ quy và chia dãy số ban đầu thành hai phần. Tiếp tục chia đến khi dãy số chỉ còn một phần tử hoặc không có phần tử nào.
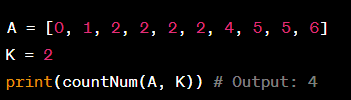
Với đầu vào là một dãy số A và một số K, hàm countNum sẽ trả về số lần xuất hiện của K trong dãy số A. Ví dụ:
Lời giải:
Để tìm vị trí thứ i trong dãy số sao cho phần tử thứ i có giá trị bằng i, ta có thể sử dụng phương pháp chia để trị như sau:
1. Tìm giá trị trung bình của left và right: mid = (left + right) // 2
2. Nếu giá trị tại vị trí mid bằng mid, tức là A[mid] == mid, thì trả về mid
3. Nếu giá trị tại vị trí mid lớn hơn mid, tức là A[mid] > mid, thì tiếp tục tìm vị trí thích hợp trong đoạn từ left đến mid-1
4. Nếu giá trị tại vị trí mid nhỏ hơn mid, tức là A[mid] < mid, thì tiếp tục tìm vị trí thích hợp trong đoạn từ mid+1 đến right
5. Nếu không tìm được vị trí thích hợp nào, tức là left > right, thì trả về -1
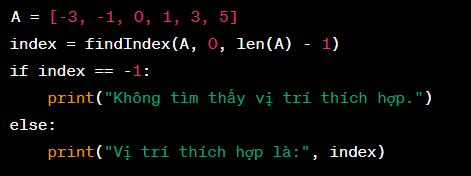
Ví dụ:
Kết quả sẽ là "Vị trí thích hợp là: 3", tức là phần tử thứ 3 trong dãy A có giá trị bằng 3.
– Hàm firstInd(A, left, right, C) sẽ tìm chỉ số của phần tử đầu tiên của dãy A có giá
trị bằng C. Nếu không sẽ trả về -1.
– Hàm lastInd(A, left, right, C) sẽ tìm chỉ số của phần tử cuối cùng của dãy A có giá trị bằng C. Nếu không thấy sẽ trả về – 1.
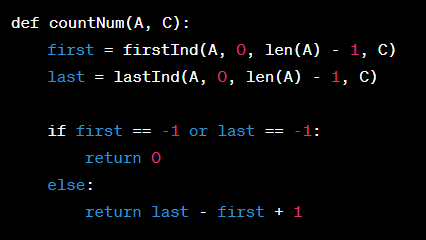
Từ hai hàm đã thiết kế trên, đưa ra một cách giải khác cho bài toán trong nhiệm vụ 1. Lời giải này có độ phức tạp O(logn).
Lời giải:
Để thiết lập hai hàm firstInd và lastInd bằng kĩ thuật chia để trị, ta có thể áp dụng phương pháp tương tự như khi tìm kiếm số lần xuất hiện của một phần tử trong dãy số bằng kĩ thuật chia để trị. Cụ thể, ta sẽ chia dãy số thành hai nửa và tìm kiếm đệ quy trên từng nửa đó.
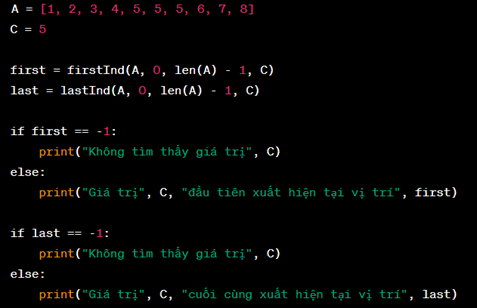
Ví dụ:
Kết quả trả về:
- Ta có thể sử dụng hàm firstInd và lastInd đã thiết kế để giải quyết bài toán tìm số lần xuất hiện của một số trong một dãy số.
Giả sử ta cần tìm số lần xuất hiện của số C trong dãy A đã sắp xếp tăng dần. Đầu tiên, ta sử dụng hàm firstInd để tìm chỉ số của phần tử đầu tiên có giá trị bằng C, sau đó sử dụng hàm lastInd để tìm chỉ số của phần tử cuối cùng có giá trị bằng C. Nếu cả hai hàm đều trả về giá trị khác -1, số lần xuất hiện của C trong dãy A sẽ là hiệu của chỉ số của phần tử cuối cùng và phần tử đầu tiên cộng thêm 1.
Vì mỗi lần gọi hàm firstInd và lastInd đều có độ phức tạp O(logn), nên độ phức tạp của giải pháp này sẽ là O(logn).
Xem thêm lời giải bài tập Chuyên đề học tập Tin học lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 6: Ý tưởng và kĩ thuật chia để trị
Bài 7: Thiết kế thuật toán theo kĩ thuật chia để trị