Bài 9.25 trang 60 SBT Toán 7 Tập 2: Xét tam giác ABC vuông tại A; đường phân giác góc B cắt cạnh AC tại E; đường thẳng qua E vuông góc với BC cắt đường thẳng AB tại K. Chứng minh:
a) AE < EC;
b) BK = BC.
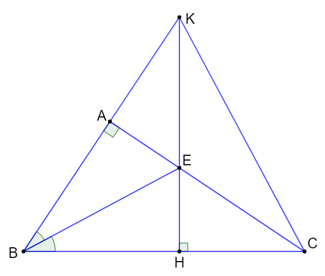
a) Đường thẳng EK cắt BC tại H.
Do E nằm trên đường thẳng BE là đường phân giác của góc KBC nên EA = EH.
Mà trong tam giác EHC là tam giác vuông tại H có EH < EC (do EC là cạnh huyền).
Từ đó ta suy ra được: AE < EC (đpcm).
b) E là giao của hai đường cao CA VÀ KH của tam giác BKC nên E là trực tâm của tam giác BKC.
Từ đó suy ra BE cũng là đường cao của tam giác BKC.
Do đó BE vừa là đường phân giác, vừa là đường cao của tam giác BKC.
Nên suy ra tam giác BKC cân tại B.
Vậy BK = BC (đpcm).
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Bài 36: Hình hộp chữ nhật và hình lập phương
Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác