Với mỗi hàm số bậc hai cho dưới đây: y = f(x) = –x^2 – x + 1; y = g(x) = x^2 – 8x + 8

Bài 6.12 trang 14 SBT Toán 10 Tập 2: Với mỗi hàm số bậc hai cho dưới đây:

y = f(x) = –x² – x + 1; y = g(x) = x² – 8x + 8;

hãy thực hiện các yêu cầu sau:

a) Viết lại hàm số bậc hai dưới dạng y = a(x – h)² + k;

b) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số;

c) Vẽ đồ thị của hàm số.

Trả lời

a)

* Xét hàm số: y = f(x) = –x² – x + 1 = –(x² + x – 1)

$$\begin{gathered} =-\left(x^2+2.\frac{1}{2}.x+\frac{1}{4}-\frac{1}{4}-1\right) \\ =-\left(x^2+2.\frac{1}{2}.x+\frac{1}{4}-\frac{5}{4}\right) \\ =-{\left(x+\frac{1}{2}\right)}^2+\frac{5}{4} \end{gathered}$$

Với a = –1, h = $-\frac{1}{2}$, k = $\frac{5}{4}$.

* Xét hàm số: y = g(x) = x² – 8x + 8 = (x² – 2.4.x + 16) – 16 + 8 = (x – 4)² – 8

Với a = 1, h = 4, k = –8.

b)

- Xét hàm số: y = f(x) = –x² – x + 1 = $-{\left(x+\frac{1}{2}\right)}^2+\frac{5}{4}$

Ta có:

${\left(x+\frac{1}{2}\right)}^2\ge 0$ với mọi số thực x

$\iff -{\left(x+\frac{1}{2}\right)}^2\le 0$ với mọi số thực x

$\iff -{\left(x+\frac{1}{2}\right)}^2+\frac{5}{4}\le \frac{5}{4}$  với mọi số thực x

$\iff f\left(x\right)\le \frac{5}{4}$ với mọi số thực x

Dấu “=” xảy ra khi x = $\frac{-1}{2}$.

Vậy giá trị lớn nhất của hàm số y = f(x) là $\frac{5}{4}$ tại x = $\frac{-1}{2}$.

- Xét hàm số: y = g(x) = x² – 8x + 8 = (x – 4)² – 8

Ta có:

(x – 4)² ≥ 0 với mọi số thực x

⇔ (x – 4)² – 8 ≥ –8  với mọi số thực x

⇔ g(x) ≥ –8 

Dấu “=” xảy ra khi x = 4.

Vậy giá trị nhỏ nhất của hàm số y = g(x) là –8 tại x = 4.

c)

- Xét hàm số: y = f(x) = –x² – x + 1

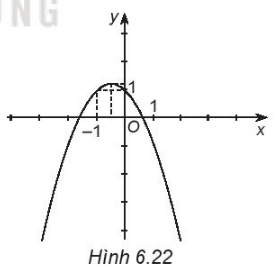
Ta có a = –1 < 0 nên parabol quay bề lõm xuống dưới.

Đỉnh $I\left(-\frac{1}{2};\frac{5}{4}\right)$.

Trục đối xứng $x=-\frac{1}{2}$.

Giao điểm với Oy là (0; 1).

Điểm đối xứng với điểm (0; 1) qua trục đối xứng $x=-\frac{1}{2}$ là (–1; 1).

Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = f(x) như hình dưới.

- Xét hàm số: y = g(x) = x² – 8x + 8

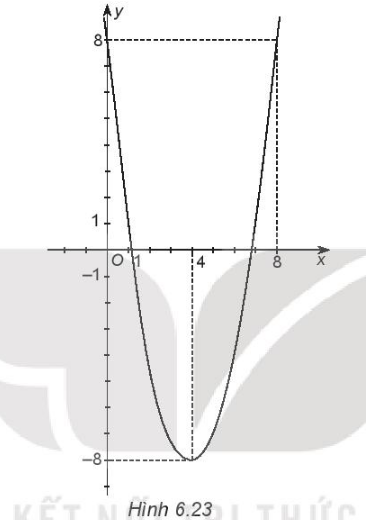
Ta có a = 1 > 0 nên parabol quay bề lõm lên trên.

Đỉnh I(4; – 8).

Trục đối xứng x = 4.

Giao điểm với Oy là (0; 8).

Điểm đối xứng với điểm (0; 8) qua trục đối xứng x = 4 là (8; 8).

Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = g(x) như hình dưới.

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 5

Bài 15: Hàm số

Bài 16: Hàm số bậc hai

Bài 17: Dấu của tam thức bậc hai

Bài 18: Phương trình quy về phương trình bậc hai

Bài tập cuối chương 6