Với giả thiết ở Bài tập 4, hãy: a) Chứng minh rằng BC // (SAD) và tính khoảng cách giữa BC và mặt phẳng (SAD)

Bài 5 trang 106 Toán 11 Tập 2: Với giả thiết ở Bài tập 4, hãy:

a) Chứng minh rằng BC // (SAD) và tính khoảng cách giữa BC và mặt phẳng (SAD).

b) Chứng minh rằng BD ⊥ (SAC) và tính khoảng cách giữa hai đường thẳng BD và SC.

Trả lời

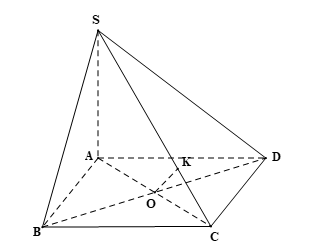
a) Do ABCD là hình vuông nên BC // AD.

Mà AD ⊂ (SAD) nên BC // (SAD).

Khi đó, d(BC, (SAD)) = d(C, (SAD)) = CD = a.

(vì theo câu a, CD ⊥ (SAD))

Vậy khoảng cách giữa BC và mặt phẳng (SAD) bằng a.

b) Vì ABCD là hình vuông nên BD ⊥ AC.

Do SA ⊥ (ABCD) và BD ⊂ (ABCD) nên SA ⊥ BD.

Ta có: BD ⊥ SA, BD ⊥ AC và SA ∩ AC = A trong (SAC).

Suy ra BD ⊥ (SAC).

Gọi O = AC ∩ BD, kẻ OK ⊥ SC (K ∈ SC).

Do BD ⊥ (SAC) và OK ⊂ (SAC) nên BD ⊥ OK.

Ta có: OK ⊥ SC và OK ⊥ BD.

Từ đó ta có đoạn thẳng OK là đoạn vuông góc chung của hai đường thẳng BD và SC nên d(BD, SC) = OK.

Do ABCD là hình vuông nên $\widehat{ABC}=90°,$ do đó tam giác ABC vuông tại B.

Áp dụng định lí Pythagore trong tam giác ABC vuông tại B có:

AC² = AB² + BC² = a² + a² = 2a².

Suy ra $AC=a\sqrt{2}.$

Do O = AC ∩ BD và AC, BD là hai đường chéo của hình vuông ABCD.

Suy ra O là trung điểm của AC nên $OC=\frac{AC}{2}=\frac{a\sqrt{2}}{2}.$

Do SA ⊥ (ABCD) và AC ⊂ (ABCD) nên SA ⊥ AC.

Áp dụng định lí Pythagore trong tam giác SAC vuông tại A (do SA ⊥ AC) có:

SC² = SA² + AC².

Do đó $SC=\sqrt{a^2+{\left(a\sqrt{2}\right)}^2}=\sqrt{a^2+2a^2}=a\sqrt{3}.$

Xét ∆SAC và ∆OKC có:

$\widehat{SAC}=\widehat{OKC}=90°;$

$\widehat{OCK}$ là góc chung

Do đó ∆SAC ᔕ ∆OKC (g.g).

Suy ra $\frac{SA}{OK}=\frac{SC}{OC}$ (tỉ số đồng dạng)

Nên $OK=\frac{SA.OC}{SC}=\frac{a.\frac{a\sqrt{2}}{2}}{a\sqrt{3}}=\frac{a\sqrt{6}}{6}.$

Khi đó $d\left(BD,SC\right)=OK=\frac{a\sqrt{6}}{6}.$

Vậy khoảng cách giữa hai đường thẳng BD và SC $\frac{a\sqrt{6}}{6}.$

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: