Cho hình lăng trụ ABC.A’B’C’ có cạnh bên bằng a, góc giữa đường thẳng AA’ và mặt phẳng (ABC) bằng 60°

Luyện tập 4 trang 104 Toán 11 Tập 2: Cho hình lăng trụ ABC.A’B’C’ có cạnh bên bằng a, góc giữa đường thẳng AA’ và mặt phẳng (ABC) bằng 60°. Tính khoảng cách giữa hai mặt phẳng (ABC) và (A’B’C’).

Trả lời

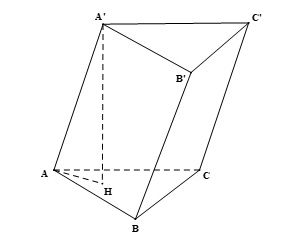
Vì ABC.A’B’C’ là hình lăng trụ nên (ABC) // (A’B’C’).

Suy ra d((ABC), (A’B’C’)) = d(A’, (ABC)). (1)

Gọi H là hình chiếu của A’ trên (ABC), tức là A’H ⊥ (ABC).

Suy ra d(A’, (ABC)) = A’H. (2)

Do A’H ⊥ (ABC) nên HA là hình chiếu của A’A trên (ABC).

Suy ra góc giữa đường thẳng A’A và mặt phẳng (ABC) bằng $\widehat{A^{\text{'}}AH}=60°.$

Ta có: A’H ⊥ (ABC) và AH ⊂ (ABC) nên A’H ⊥ AH.

Xét tam giác A’HA vuông tại H (vì A’H ⊥ AH) có:

$\sin \widehat{A^{\text{'}}AH}=\frac{A^{\text{'}}H}{A{A}^{\text{'}}}\Rightarrow A^{\text{'}}H=A{A}^{\text{'}}.\sin \widehat{A^{\text{'}}AH}=a.\sin 60°=\frac{a\sqrt{3}}{2}.$

Kết hợp với (1) và (2) ta có: $d\left(\left(ABC\right),\left(A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}\right)\right)=d\left(A^{\text{'}},\left(ABC\right)\right)=A^{\text{'}}H=\frac{a\sqrt{3}}{2}.$

Vậy khoảng cách giữa hai mặt phẳng (ABC) và (A’B’C’) bằng $\frac{a\sqrt{3}}{2}.$

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: