Cho hình chóp S.ABC có SA ⊥ (ABC), AI ⊥ BC (I ∈ BC), AH ⊥ SI (H ∈ SI). Chứng minh rằng khoảng cách từ A đến mặt phẳng (SBC) bằng AH
200
09/12/2023
Luyện tập 1 trang 101 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), AI ⊥ BC (I ∈ BC), AH ⊥ SI (H ∈ SI). Chứng minh rằng khoảng cách từ A đến mặt phẳng (SBC) bằng AH.
Trả lời
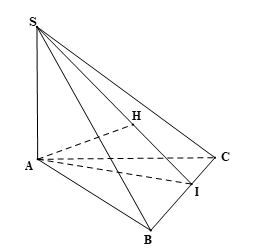
Do SA ⊥ (ABC) và BC ⊂ (ABC) nên SA ⊥ BC.
Ta có: BC ⊥ SA, BC ⊥ AI và SA ∩ AI = A trong (SAI).
Suy ra BC ⊥ (SAI).
Mà AH ⊂ (SAI) nên BC ⊥ AH.
Ta có: AH ⊥ BC, AH ⊥ SI và BC ∩ SI = I trong (SBC).
Suy ra AH ⊥ (SBC).
Ta thấy H ∈ (SBC) và AH ⊥ (SBC) nên khoảng cách từ A đến mặt phẳng (SBC) bằng AH.
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:

