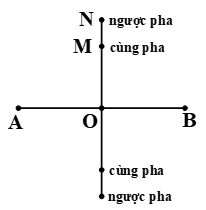
Trong thí nghiệm giao thoa sóng mặt nước, hai nguồn đặt tại hai điểm \({\rm{A}},{\rm{B}}\) ở mặt nước dao động điều hòa theo phương thẳng đứng, cùng pha tạo ra hai sóng kết hợp có bước sóng \(4{\rm{\;cm}}\). Khoảng cách giữa hai nguồn \({\rm{AB}} = 30{\rm{\;cm}}\). Hai điểm \({\rm{M}},{\rm{N}}\) ở mặt nước nằm trên trung trực của \({\rm{AB}}\) là hai điểm liên tiếp mà phần tử nước ở \({\rm{M}}\) dao động cùng pha với nguồn, phần tử ở \({\rm{N}}\) dao động ngược pha với nguồn. Khoảng cách lớn nhất của \({\rm{MN}}\) gần nhất với giá trị nào sau đây?

\(OA = OB = \frac{{AB}}{2} = \frac{{30}}{2} = 15cm = 3,75\lambda \to \left\{ \begin{array}{l}MA = 4\lambda = 4.4 = 16cm\\NA = 4,5\lambda = 4,5.4 = 18cm\end{array} \right.\)

Vì M và N là hai điểm liên tiếp nên M và N phải nằm cùng phía

\(M{N_{\max }} = ON - OM = \sqrt {N{A^2} - O{A^2}} - \sqrt {M{A^2} - O{A^2}} = \)

\( = \sqrt {{{18}^2} - {{15}^2}} - \sqrt {{{16}^2} - {{15}^2}} \approx 4,4cm\). Chọn A