Hai vật nhỏ có cùng khối lượng 100 g dao động điều hòa trên hai đường thẳng
Hai vật nhỏ có cùng khối lượng 100g dao động điều hòa trên hai đường thẳng song song với nhau, cách nhau 10cm, vị trí cân bằng của hai vật cùng nằm trên đường vuông góc với hai quỹ đạo. Hình vẽ bên là đồ thị biểu diễn động năng của mỗi vật theo thời gian. Tại thời điểm mà li độ của vật thứ nhất đạt cực đại thì khoảng cách giữa hai vật gần nhất với giá trị nào sau đây?
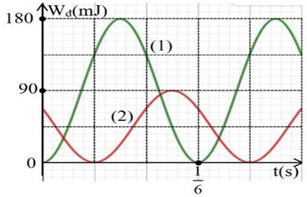
A. 13cm.
B. 12cm.
C. 14cm.
D. 11cm,
