Câu hỏi:
31/01/2024 61
Trong một tam giác, trực tâm là giao điểm của ba đường nào?
Trong một tam giác, trực tâm là giao điểm của ba đường nào?
A. Đường phân giác;
A. Đường phân giác;
B. Đường trung tuyến;
B. Đường trung tuyến;
C. Đường trung trực;
C. Đường trung trực;
D. Đường cao.
D. Đường cao.
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Trong một tam giác, trực tâm là giao điểm của ba đường cao.
Đáp án đúng là: D
Trong một tam giác, trực tâm là giao điểm của ba đường cao.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.
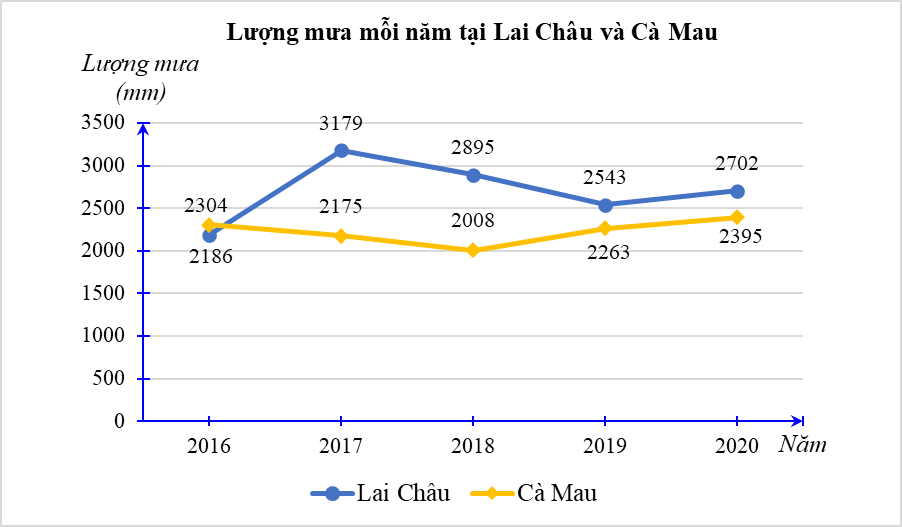
Chọn ngẫu nhiên 1 năm trong 5 năm đó. Tính xác suất của các biến cố sau:
A: “Tại năm được chọn, lượng mưa ở Cà Mau cao hơn ở Lai Châu”;
B: “Tại năm được chọn, lượng mưa ở Cà Mau thấp hơn 25 m”;
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.
Chọn ngẫu nhiên 1 năm trong 5 năm đó. Tính xác suất của các biến cố sau:
A: “Tại năm được chọn, lượng mưa ở Cà Mau cao hơn ở Lai Châu”;
B: “Tại năm được chọn, lượng mưa ở Cà Mau thấp hơn 25 m”;
Câu 2:
A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Xác định bậc và hệ số cao nhất của đa thức A(x).
A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Xác định bậc và hệ số cao nhất của đa thức A(x).
Câu 3:
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.
Tính tổng lượng mưa tại mỗi tỉnh Lai Châu và Cà Mau trong giai đoạn 2016 – 2020.
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.
Câu 4:
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.
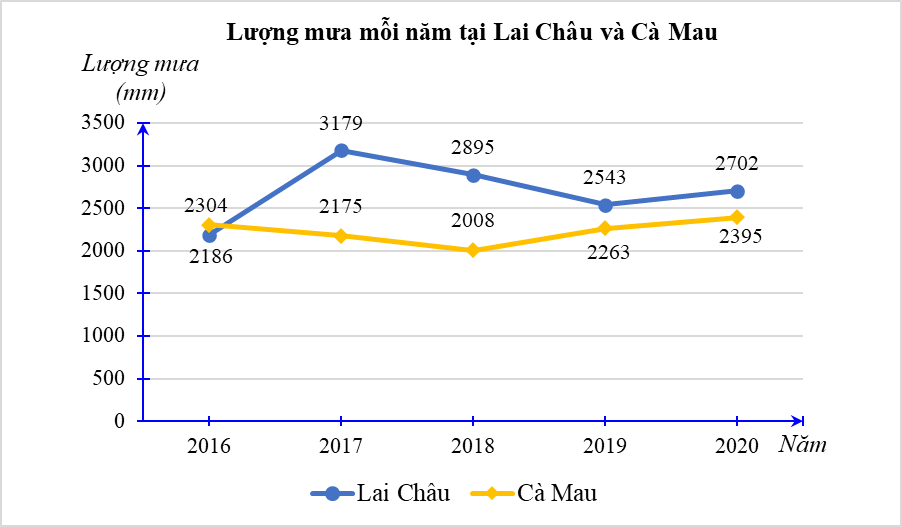
Năm 2017, lượng mưa tại Cà Mau bằng bao nhiêu phần trăm lượng mưa tại Lai Châu (làm tròn kết quả với độ chính xác 0,005)?
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.
Năm 2017, lượng mưa tại Cà Mau bằng bao nhiêu phần trăm lượng mưa tại Lai Châu (làm tròn kết quả với độ chính xác 0,005)?
Câu 5:
Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Tìm đa thức A(x)
Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Tìm đa thức A(x)Câu 6:
Tung hai con xúc xắc màu xanh và đỏ rồi quan sát số chấm xuất hiện trên mặt hai con xúc xắc. Xét biến cố A: “Số chấm trên mặt hai con xúc xắc bằng nhau”. Khẳng định nào sau đây là đúng?
Tung hai con xúc xắc màu xanh và đỏ rồi quan sát số chấm xuất hiện trên mặt hai con xúc xắc. Xét biến cố A: “Số chấm trên mặt hai con xúc xắc bằng nhau”. Khẳng định nào sau đây là đúng?
Câu 7:
Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Tìm đa thức M(x) sao cho M(x) = A(x).B(x) biết B(x) = –x2 + x.
Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Tìm đa thức M(x) sao cho M(x) = A(x).B(x) biết B(x) = –x2 + x.
Câu 8:
Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Tính M(‒1), từ đó kết luận số ‒1 có phải là nghiệm của đa thức M(x) hay không.
Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Tính M(‒1), từ đó kết luận số ‒1 có phải là nghiệm của đa thức M(x) hay không.
Câu 9:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
DABD = DEBD từ đó suy ra AD = ED.
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
DABD = DEBD từ đó suy ra AD = ED.
Câu 10:
Cho các dãy dữ liệu:
(1) Tên của mỗi bạn học sinh trong lớp 7A.
(2) Số lượng học sinh của các lớp 7 đạt điểm 10 thi giữa học kì I.
(3) Số nhà của mỗi bạn học sinh lớp 7B.
(4) Số lượng nhóm nhạc yêu thích của mỗi bạn học sinh trong lớp.
Trong các dãy dữ liệu trên, dãy dữ không phải là số là
Cho các dãy dữ liệu:
(1) Tên của mỗi bạn học sinh trong lớp 7A.
(2) Số lượng học sinh của các lớp 7 đạt điểm 10 thi giữa học kì I.
(3) Số nhà của mỗi bạn học sinh lớp 7B.
(4) Số lượng nhóm nhạc yêu thích của mỗi bạn học sinh trong lớp.
Trong các dãy dữ liệu trên, dãy dữ không phải là số là
Câu 12:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
BD là đường trung trực của đoạn thẳng AE và AD < DC.
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
BD là đường trung trực của đoạn thẳng AE và AD < DC.
Câu 13:
Xác định các hằng số a và b sao cho đa thức x4 + ax2 + b chia hết cho đa thức x2 – x + 1
Câu 15:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
Ba điểm E, D, F thẳng hàng.
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
Ba điểm E, D, F thẳng hàng.
