Câu hỏi:
03/04/2024 36
Trong mặt phẳng tọa độ Oxy, cho \(\Delta :x - 2y - 1 = 0\) và \(\overrightarrow u \left( {4;3} \right)\). Gọi \(d\) là đường thẳng sao cho \({T_{\overrightarrow u }}\) biến \(d\) thành đường thẳng \(\Delta \). Phương trình đường thẳng \(d\) là
A. \(x - 2y + 1 = 0\).
B. \(x - 2y + 9 = 0\).
C. \(x - 2y - 3 = 0\).
D. \(x - 2y - 9 = 0\).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Phương pháp:
Phép tính tiến biến đường thẳng thành đường thẳng song song với nó.
Cách giải:
Vì \(\Delta = {T_{\overrightarrow u }}\left( d \right) \Rightarrow \Delta ||d\) Þ Phương trình \(\Delta \) có dạng: \(x - 2y + c = 0\left( \Delta \right)\).
Lấy \(A\left( {1;0} \right)\) bất kì thuộc \(d\). Gọi \(A' = {T_{\overrightarrow u }}\left( A \right) \Rightarrow A' \in \Delta \).
Ta có: \(A' \in {T_{\overrightarrow u }}\left( A \right) \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = {x_A} + {x_{\overrightarrow u }} = 1 + 4 = 5\\{y_{A'}} = {y_A} + {y_{\overrightarrow u }} = 0 + 3 = 3\end{array} \right. \Rightarrow A'\left( {5;3} \right)\).
Vì \(A' \in \Delta \Rightarrow 5 - 2.3 + c = 0 \Leftrightarrow c = 1\).
Vậy phương trình đường thẳng \(\Delta \) là: \(x - 2y + 1 = 0\).
Đáp án A
Phương pháp:
Phép tính tiến biến đường thẳng thành đường thẳng song song với nó.
Cách giải:
Vì \(\Delta = {T_{\overrightarrow u }}\left( d \right) \Rightarrow \Delta ||d\) Þ Phương trình \(\Delta \) có dạng: \(x - 2y + c = 0\left( \Delta \right)\).
Lấy \(A\left( {1;0} \right)\) bất kì thuộc \(d\). Gọi \(A' = {T_{\overrightarrow u }}\left( A \right) \Rightarrow A' \in \Delta \).
Ta có: \(A' \in {T_{\overrightarrow u }}\left( A \right) \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = {x_A} + {x_{\overrightarrow u }} = 1 + 4 = 5\\{y_{A'}} = {y_A} + {y_{\overrightarrow u }} = 0 + 3 = 3\end{array} \right. \Rightarrow A'\left( {5;3} \right)\).
Vì \(A' \in \Delta \Rightarrow 5 - 2.3 + c = 0 \Leftrightarrow c = 1\).
Vậy phương trình đường thẳng \(\Delta \) là: \(x - 2y + 1 = 0\).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian cho 10 điểm phân biệt, trong đó không có 4 điểm nào đồng phẳng. Số các hình tứ diện có thể kẻ được là:
Câu 2:
Cho số tự nhiên \(n\) thỏa mãn \(A_n^2 = 132\). Giá trị của \(n\) là:
Câu 3:
Gieo ngẫu nhiên 3 con súc sắc cân đối, đồng chất. Xác suất để tích số chấm xuất hiện trên ba con súc sắc là một số tự nhiên chẵn là:
Câu 4:
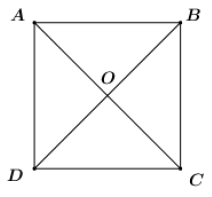
Cho hình vuông ABCD tâm O. Ảnh của đường thẳng CD qua phép quay tâm O, góc quay -90° là:

Câu 5:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên có 4 chữ số?
Câu 6:
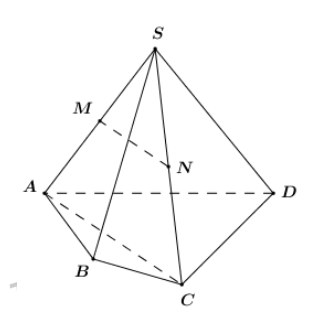
Cho hình chóp \(S.ABCD\). Gọi \(M\)và \(N\) lần lượt là trung điểm của \(SA\) và \(SC\). Khẳng định nào sau đây là đúng?

Câu 7:
Hệ số của \({x^5}\) trong khai triển \(P\left( x \right) = x{\left( {1 - 2x} \right)^5} + {x^2}{\left( {1 + 3x} \right)^{10}}\) là:
Câu 8:
Mỗi tổ có 5 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh để làm trực nhật. Tính xác suất để 3 học sinh được chọn có cả nam và nữ.
Câu 9:
Cho hình chóp S.ABCD có ABCD là hình thang cân đáy lớn AD. Gọi M, N, P lần lượt là trung điểm của AB, CD, SB. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {MNP} \right)\) là
Câu 10:
Từ các số 1, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên chẵn có 4 chữ số đôi một khác nhau?
Câu 11:
Hệ số của \[{x^{12}}\]trong khai triển \[{\left( {{x^2} + x} \right)^{10}}\] là
Câu 13:
Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AD\) là đáy lớn thỏa mãn \(AD = 2BC\). Các điểm \(M,N\) lần lượt là trung điểm của các cạnh \(SA,\,\,SD\).
a) Chứng minh đường thẳng \(MN\) song song với mặt phẳng \(\left( {SBC} \right)\).
b) Mặt phẳng \(\left( {MCD} \right)\) cắt \(SB\) tại \(E\). Tính tỉ số \(\frac{{SE}}{{EB}}\).
Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AD\) là đáy lớn thỏa mãn \(AD = 2BC\). Các điểm \(M,N\) lần lượt là trung điểm của các cạnh \(SA,\,\,SD\).
a) Chứng minh đường thẳng \(MN\) song song với mặt phẳng \(\left( {SBC} \right)\).
b) Mặt phẳng \(\left( {MCD} \right)\) cắt \(SB\) tại \(E\). Tính tỉ số \(\frac{{SE}}{{EB}}\).