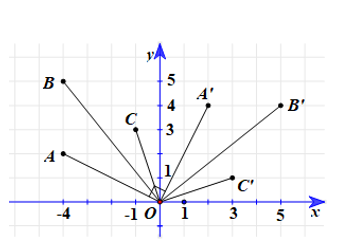
Trong mặt phẳng tọa độ Oxy, cho các điểm A(–4; 2), B(–4; 5) và C(–1; 3). a) Chứng minh các điểm A’(2; 4), B’(5; 4) và C’(3; 1) theo thứ tự là ảnh của A, B, C qua phép quay tâm O với góc quay
19
10/08/2024
Trong mặt phẳng tọa độ Oxy, cho các điểm A(–4; 2), B(–4; 5) và C(–1; 3).
a) Chứng minh các điểm A’(2; 4), B’(5; 4) và C’(3; 1) theo thứ tự là ảnh của A, B, C qua phép quay tâm O với góc quay –90°.
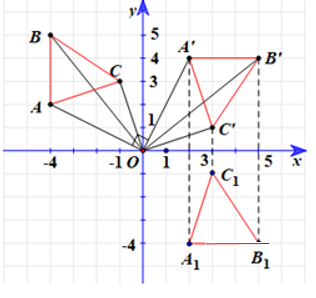
b) Gọi ∆A1B1C1 là ảnh của ∆ABC qua phép dời hình có được bằng cách thực hiện phép quay tâm O với góc quay –90° và phép đối xứng qua Ox. Tìm tọa độ các đỉnh của ∆A1B1C1.
Trả lời
a)
Với A(–4; 2) và A’(2; 4), ta có .
Do đó và .
Suy ra .
Do đó .
Mà khi quay đoạn OA (với tâm O) theo hướng cùng chiều kim đồng hồ một góc 90° thì ta được đoạn OA’. Tức là, phép quay có góc quay lượng giác theo chiều âm một góc 90°.
Vì vậy góc lượng giác (OA, OA’) = –90°.
Vậy A’ là ảnh của A qua phép quay tâm O với góc quay –90°.
Chứng minh tương tự, ta thu được B’, C’ theo thứ tự là ảnh của B, C qua phép quay tâm O với góc quay –90°.
b) Từ câu a, ta có phép quay tâm O, góc quay –90° biến ∆ABC thành ∆A’B’C’.
Ta có: ∆A1B1C1 là ảnh của ∆A’B’C’ qua phép đối xứng trục Ox nên:
• A1 = ĐOx(A’), do đó hai điểm A1 và A’(2; 4) có cùng hoành độ và có tung độ đối nhau, suy ra A1(2; –4).
• B1 = ĐOx(B’), do đó hai điểm B1 và B’(5; 4) có cùng hoành độ và có tung độ đối nhau, suy ra B1(5; –4).
• C1 = ĐOx(C’), do đó hai điểm C1 và C’(3; 1) có cùng hoành độ và có tung độ đối nhau, suy ra C1(3; –1).
Vậy tọa độ các đỉnh của ∆A1B1C1 thỏa mãn yêu cầu bài toán là A1(2; –4), B1(5; –4), C1(3; –1).