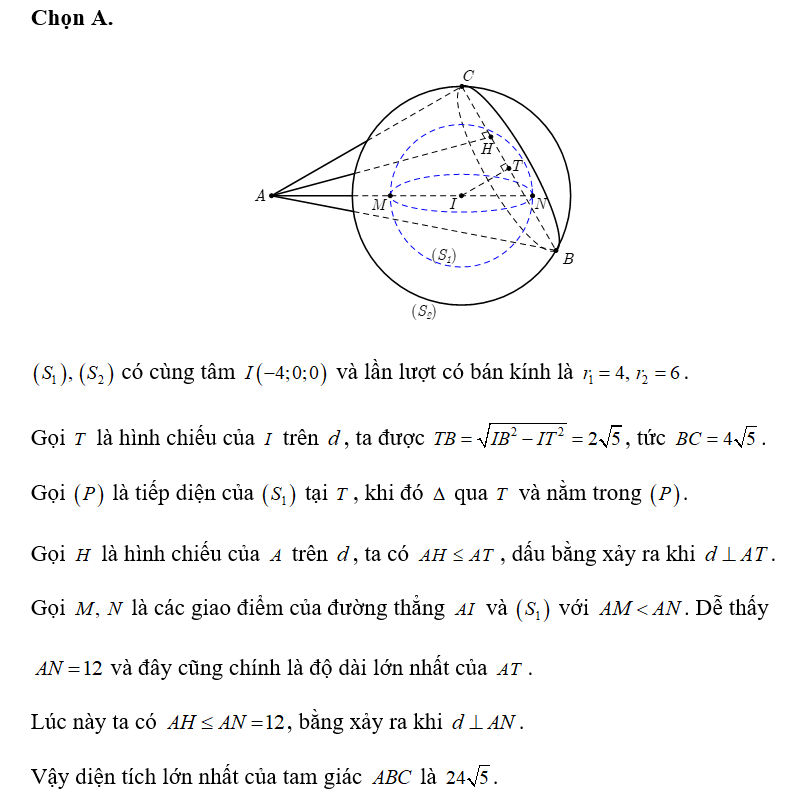
Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu (S1): (x+4)^2+ y^2+z^2=16

Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu $\left(S_1\right):{\left(x+4\right)}^2+y^2+z^2=16$, $\left(S_2\right):{\left(x+4\right)}^2+y^2+z^2=36$ và điểm A(4;0;0). Đường thẳng $\Delta$ di động nhưng luôn tiếp xúc với $\left(S_1\right)$, đồng thời cắt $\left(S_2\right)$ tại hai điểm B,C. Tam giác ABC có thể có diện tích lớn nhất là bao nhiêu?

Trả lời