Cho các hàm số  f(x) = mx^4+ mx^3+ px^2+ qx + r

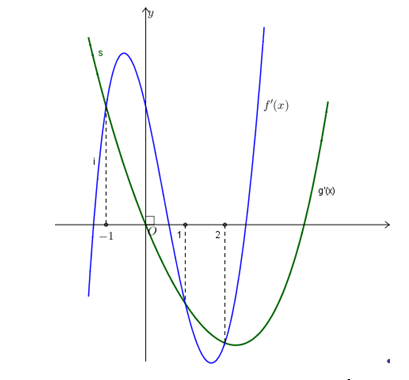
Cho các hàm số $f\left(x\right)=m{x}^4+n{x}^3+p{x}^2+qx+r$ và $g\left(x\right)=a{x}^3+b{x}^2+cx+d \left(m,n,p,q,r,a,b,c,d\in ℝ\right)$ thỏa mãn $f\left(0\right)=g\left(0\right)$. Các hàm số y = f'(x) và y= g'(x) có đồ thị như hình vẽ bên.

Gọi S là tổng tất cả nghiệm của phương trình $f\left(x\right)=g\left(x\right)$. Khi đó mệnh đề nào sau đây đúng?

Trả lời

Ta có $f\left(x\right)=g\left(x\right)\iff a{x}^3+b{x}^2+cx+d=m{x}^4+n{x}^3+p{x}^2+qx+r.$

$\iff m{x}^4+\left(n-a\right)x^3+\left(p-b\right)x^2+\left(q-c\right)x+r-d=0\left(1\right)$

Do $f\left(0\right)=g\left(0\right)\Rightarrow x=0$ là nghiệm của phương trình $\left(1\right)\Rightarrow r-d=0.$

Lại có $f\text{'}\left(x\right)=4m{x}^3+3n{x}^2+2px+q.g\text{'}\left(x\right)=3a{x}^2+2bx+c$.

$f\text{'}\left(x\right)=g\text{'}\left(x\right)\iff 4m{x}^3+3\left(n-a\right)x^2+2\left(p-b\right)x+q=0$.

Từ đồ thị suy ra $m>0,a>0,g\text{'}\left(0\right)=0\Rightarrow c=0.$

Ngoài ra, phương trình $f\text{'}\left(x\right)=g\text{'}\left(x\right)$ có các nghiệm $x=-a;x=1;x=2$ nên ta có hệ:

$\left\{\begin{array}{l}-4m+3\left(n-a\right)-2\left(p-b\right)+q=0\\ 4m+3\left(n-a\right)+2\left(p-b\right)+q=0\\ 32m+12\left(n-a\right)+4\left(p-b\right)+q=0\end{array}\right.\iff \left\{\begin{array}{l}p-b=-2m\\ q=-3\left(n-a\right)\\ 32m-4q-8m+q=0\end{array}\right.\iff \left\{\begin{array}{l}p-b=-2m\\ n-a=-\frac{8}{3}m\\ q=8m\end{array}\right.$

Khi đó phương trình (1) thành

$\iff m{x}^4-\frac{8}{3}m{x}^3-2m{x}^2+8mx=0\iff x^4-\frac{8}{3}{x}^3-2x^2+8x=0\iff x\left(x^3-\frac{8}{3}{x}^2-2x+8\right)=0\iff \left[\begin{array}{l}x=0\\ x^3-\frac{8}{3}{x}^2-2x+8=0\left(2\right)\end{array}\right.$

Xét $h\left(x\right)=x^3-\frac{8}{3}{x}^2-2x+8$, tập xác định $\mathrm{ℝ}$

$h\text{'}\left(x\right)=3x^2-\frac{16}{3}x-2=0\iff \left[\begin{array}{l}x=\frac{8+\sqrt{118}}{9}=x_1\\ x=\frac{8-\sqrt{118}}{9}=x_2\end{array}\right.$

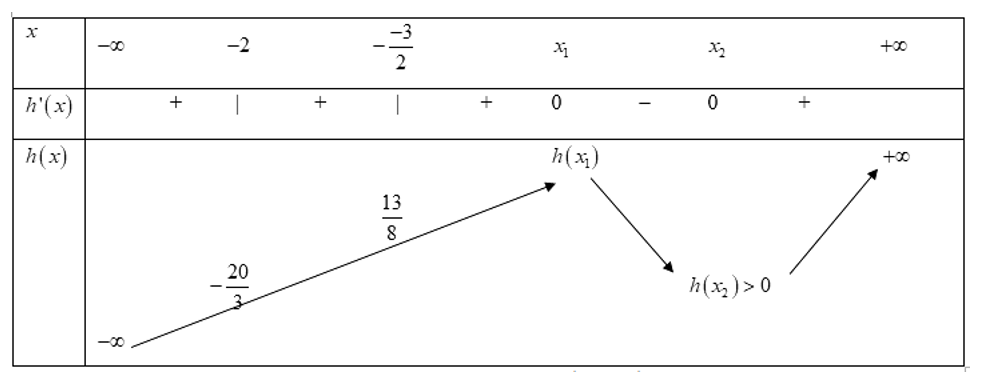
Bảng biến thiên

Suy ra, phương trình (2) có 1 nghiệm duy nhất trong khoảng $\left(-2;-\frac{3}{2}\right)$ nên phương trình (1) có 2 nghiệm x=0 và $x\in \left(-2;-\frac{3}{2}\right).$ Do đó, tổng tất cả các nghiệm của phương trình $\left(1\right):S\in \left(-2;-\frac{3}{2}\right).$

Chọn C.