Trong Hình 4.78, ta có AN = BM, góc BAN = góc ABM. Chứng minh rằng góc BAM= góc ABN
Bài 4.36 trang 87 Toán 7 Tập 1: Trong Hình 4.78, ta có AN = BM, ^BAN=^ABM. Chứng minh rằng ^BAM=^ABN.
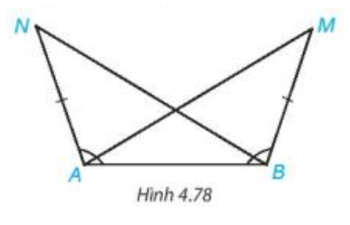
Bài 4.36 trang 87 Toán 7 Tập 1: Trong Hình 4.78, ta có AN = BM, ^BAN=^ABM. Chứng minh rằng ^BAM=^ABN.

|
GT |
AN = BM, ^BAN=^ABM. |
|
KL |
^BAM=^ABN. |
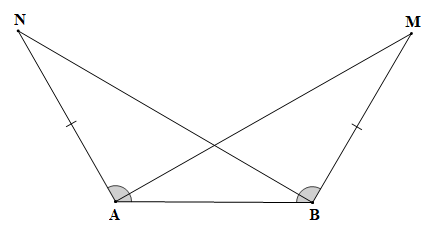
Xét tam giác ABN và tam giác BAM có:
AN = BM (theo giả thiết);
^BAN=^ABM (theo giả thiết);
AB là cạnh chung.
Vậy ΔABN=ΔBAM (c.g.c).
Suy ra ^ABN=^BAM (hai góc tương ứng).
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Bài tập cuối chương 4 trang 87
Bài 17: Thu thập và phân loại dữ liệu