Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN
901
22/10/2023
Bài 4.37 trang 87 Toán 7 Tập 1: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.
Trả lời
|
GT
|
M, N thuộc đường trung trực của AB
AM = AN
|
|
KL
|
MB = NB
^AMB=^ANB
|
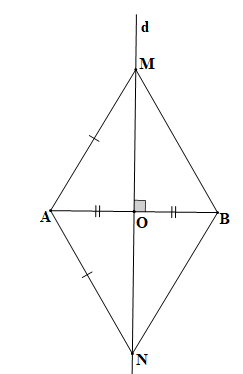
M và N là hai điểm phân biệt nằm trên đường trung trực của AB với AM = AN nên M và N có vị trí như hình vẽ trên.
Gọi O là giao điểm của AB và MN, d là đường trung trực của AB nên d⊥AB tại trung điểm O của AB.
Xét tam giác OAM (vuông tại O) và tam giác OAN (vuông tại O) có:
OA là cạnh chung;
AM = AN (theo giả thiết).
Vậy ΔOAM=ΔOAN (cạnh huyền – cạnh góc vuông).
Suy ra OM = ON (hai cạnh tương ứng) và ^AMO=^ANO (hai góc tương ứng).
Xét tam giác OBM (vuông tại O) và tam giác OBN (vuông tại O) có:
OB là cạnh chung;
OM = ON (chứng minh trên).
Vậy ΔOBM=ΔOBN (hai cạnh góc vuông).
Suy ra MB = NB (hai cạnh tương ứng) và ^BMO=^BNO (hai góc tương ứng).
Ta có ^AMO=^ANO (chứng minh trên) và ^BMO=^BNO (chứng minh trên) nên ^AMO+^BMO=^ANO+^BNO.
Mà ^AMB=^AMO+^BMO và ^ANB=^ANO+^BNO.
Suy ra ^AMB=^ANB.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Luyện tập chung trang 86
Bài tập cuối chương 4 trang 87
Bài 17: Thu thập và phân loại dữ liệu
Bài 18: Biểu đồ hình quạt tròn
Bài 19: Biểu đồ đoạn thẳng

