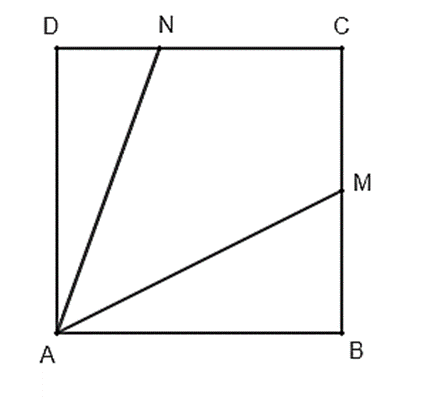
Trên một mảnh đất hình vuông ABCD Tính tan(góc BAM + góc DAN)
26
01/08/2024
Trên một mảnh đất hình vuông ABCD, bác An đặt một chiếc đèn pin tại vị trí A chiếu chùm sáng phân kì sang phía góc C. Bác An nhận thấy góc chiếu sáng của đèn pin giới hạn bởi hai tia AM và AN, ở đó các điểm M, N lần lượt thuộc các cạnh BC, CD sao cho BM = \(\frac{1}{2}\)BC, DN = \(\frac{1}{3}\)DC (Hình 4).
Tính \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)\).
Trả lời
Trong tam giác vuông ABM, có \(\tan \widehat {BAM} = \frac{{BM}}{{BA}} = \frac{1}{2}\).
Trong tam giác vuông ADN, có \(\tan \widehat {DAN} = \frac{{DN}}{{AD}} = \frac{{DN}}{{DC}} = \frac{1}{3}\).
Do đó, \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)\)\( = \frac{{\tan \widehat {BAM} + \tan \widehat {DAN}}}{{1 - \tan \widehat {BAM}.\tan \widehat {DAN}}}\)\( = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 - \frac{1}{2}.\frac{1}{3}}} = 1\).