Câu hỏi:
26/01/2024 71
Quan sát hình vẽ dưới đây.
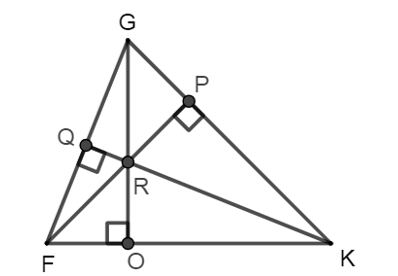
Khẳng định nào dưới đây là sai?
Quan sát hình vẽ dưới đây.

Khẳng định nào dưới đây là sai?
A. Trực tâm của ∆FRK là G;
A. Trực tâm của ∆FRK là G;
B. Trực tâm của ∆FPK là O;
B. Trực tâm của ∆FPK là O;
C. Trực tâm của ∆GFK là R;
D. Cả A và C đều đúng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: B
∆FRK có RG ⊥ FK, KG ⊥ FR và RG cắt KG tại G nên G là trực tâm của ∆FRK.
∆FPK vuông tại P nên trực tâm của ∆FPK là P.
∆GFK có GO ⊥ FK, FP ⊥ GK và GO cắt FP tại R nên R là trực tâm của ∆GFK.
Vậy ta chọn phương án B.
Hướng dẫn giải:
Đáp án đúng là: B
∆FRK có RG ⊥ FK, KG ⊥ FR và RG cắt KG tại G nên G là trực tâm của ∆FRK.
∆FPK vuông tại P nên trực tâm của ∆FPK là P.
∆GFK có GO ⊥ FK, FP ⊥ GK và GO cắt FP tại R nên R là trực tâm của ∆GFK.
Vậy ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC vuông tại A, trên tia BA lấy M sao cho BM = BC. Tia phân giác góc B cắt AC tại H. Khẳng định nào sau đây là sai?
Câu 2:
Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N. Từ C kẻ đường thẳng vuông góc với BM tại P. Gọi D là giao điểm của AB và CP. Khẳng định nào sau đây sai?
Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N. Từ C kẻ đường thẳng vuông góc với BM tại P. Gọi D là giao điểm của AB và CP. Khẳng định nào sau đây sai?
Câu 3:
Cho ∆ABC vuông cân tại A, lấy E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Trực tâm của ∆BCD là điểm nào?
Cho ∆ABC vuông cân tại A, lấy E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Trực tâm của ∆BCD là điểm nào?
Câu 4:
Cho ∆ABC cân tại A, đường trung tuyến AD và đường cao BK cắt nhau tại E. Khẳng định nào dưới đây là đúng?
Cho ∆ABC cân tại A, đường trung tuyến AD và đường cao BK cắt nhau tại E. Khẳng định nào dưới đây là đúng?
Câu 6:
Trên đường thẳng d có ba điểm phân biệt I, J, K (J ở giữa I và K). Lấy điểm M nằm ngoài đường thẳng d sao cho MJ vuông góc với d tại J. Đường thẳng qua I vuông góc với MK cắt MJ tại N. Điểm nào là trực tâm của tam giác MIK?
Trên đường thẳng d có ba điểm phân biệt I, J, K (J ở giữa I và K). Lấy điểm M nằm ngoài đường thẳng d sao cho MJ vuông góc với d tại J. Đường thẳng qua I vuông góc với MK cắt MJ tại N. Điểm nào là trực tâm của tam giác MIK?