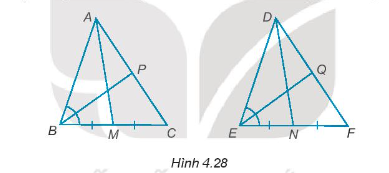
Cho tam giác ABC bằng tam giác DEF (H.4.28). a) Gọi M và N lần lượt là trung điểm các đoạn thẳng BC và EF
226
09/12/2023
Bài 4.28 trang 62 Tập 1: Cho tam giác ABC bằng tam giác DEF (H.4.28).
a) Gọi M và N lần lượt là trung điểm các đoạn thẳng BC và EF. Chứng minh rằng AM = DN.
b) Trên hai cạnh AC và DF lấy hai điểm P và Q sao cho BP, EQ lần lượt là phân giác của các góc và . Chứng minh rằng: BP = EQ.
Trả lời
a) Vì ∆ABC = ∆DEF nên
Vì M là trung điểm của BC nên BM = MC = .
Vì N là trung điểm của EF nên EN = NF = .
Mà BC = EF (chứng minh trên) nên BM = EN.
Xét ∆ABM và ∆DEN ta có:
BM = EN (chứng minh trên)
AB = DE (chứng minh trên)
(do chứng minh trên)
Do đó, ∆ABM = ∆DEN (c – g – c).
Suy ra, AM = DN (hai cạnh tương ứng).
b) Vì BP là tia phân giác của góc nên
Vì EQ là tia phân giác của góc nên
Mà = nên = .
Xét ∆PBC và ∆QEF ta có:
BC = EF (chứng minh trên)
= (chứng minh trên)
(do chứng minh trên)
Do đó, ∆PBC = ∆QEF (g – c – g)
Suy ra, BP = EQ (hai cạnh tương ứng).
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 12: Tổng các góc trong một tam giác
Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Ôn tập chương 4

