Ở mặt nước, tại hai điểm S1 và S2 có hai nguồn sóng kết hợp, dao động điều hòa, cùng pha theo phương thẳng đứng. Biết sóng truyền trên mặt nước với bước sóng lambda, khoảng cách S1S2 = 5,6lam
70
08/06/2024
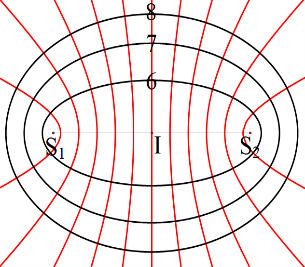
Ở mặt nước, tại hai điểm \({S_1}\) và \({S_2}\) có hai nguồn sóng kết hợp, dao động điều hòa, cùng pha theo phương thẳng đứng. Biết sóng truyền trên mặt nước với bước sóng \(\lambda \), khoảng cách \({S_1}{S_2} = 5,6\lambda \). Ở mặt nước, gọi \({\rm{M}}\) là vị trí mà phần tử nước tại đó dao động với biên độ cực đại, cùng pha với dao động của hai nguồn. Khoảng cách ngắn nhất từ \({\rm{M}}\) đến đường thẳng \({S_1}{S_2}\) là
A. \(0,868\lambda \)
B. \(0,946\lambda \)
C. \(0,852\lambda \)
D. \(0,754\lambda \)
Trả lời
Hướng dẫn
Chuẩn hóa \(\lambda = 1\). M gần \({S_1}{S_2}\) nhất thì M phải nằm trên đường cực đại gần nguồn nhất và phải nằm trên elip nhỏ nhất. Nhưng vì đường cực đại gần nguồn nhất là \({k_1} - {k_2} = 5\) không cùng tính chất chẵn lẻ với đường elip nhỏ nhất là \({k_1} + {k_2} = 6\) nên ta phải xét riêng 2 trường hợp rồi so sánh
TH1: \(\left\{ \begin{array}{l}{k_1} - {k_2} = 5\\{k_1} + {k_2} = 7\end{array} \right. \Rightarrow y = \sqrt {{R^2} - {x^2}} = \sqrt {\frac{{{5^2} + {7^2} - {{5,6}^2}}}{4} - {{\left( {\frac{{5.7}}{{2.5,6}}} \right)}^2}} \approx 0,946\)
TH2: \(\left\{ \begin{array}{l}{k_1} - {k_2} = 4\\{k_1} + {k_2} = 6\end{array} \right. \Rightarrow y = \sqrt {{R^2} - {x^2}} = \sqrt {\frac{{{4^2} + {6^2} - {{5,6}^2}}}{4} - {{\left( {\frac{{4.6}}{{2.5,6}}} \right)}^2}} \approx 0,754\). Chọn D