Nhận biết tiếp tuyến của đồ thị hàm số Cho hàm số y = f(x) có đồ thị (C) và P(x0; f(x0)) ∈ (C). Xét điểm Q(x; f(x)) thay đổi trên (C) với x ≠ x0. a) Đường thẳng đi qua hai điểm P, Q được g
Nhận biết tiếp tuyến của đồ thị hàm số
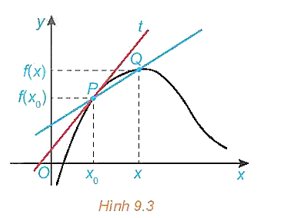
Cho hàm số y = f(x) có đồ thị (C) và P(x0; f(x0)) ∈ (C). Xét điểm Q(x; f(x)) thay đổi trên (C) với x ≠ x0.
a) Đường thẳng đi qua hai điểm P, Q được gọi là một cát tuyến của đồ thị (C) (H.9.3). Tìm hệ số góc kPQ của cát tuyến PQ.
