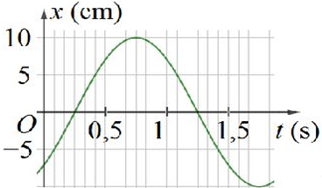
Một vật dao động điều hòa với phương trình \(x = A\cos (\omega t + \varphi )\). Hình bên là đồ thị biểu diễn sự phụ thuộc li độ \(x\) theo thời gian \(t\). Tại thời điểm \(t = 0\), gia tốc của vật có giá trị là

B. \( - 5\sqrt 3 {\pi ^2}\;cm/{s^2}\).

D. \(5\sqrt 3 {\pi ^2}\;cm/{s^2}\).

Đáp án C:

\(\frac{T}{4} = 6\hat o = 0,5s \Rightarrow T = 2s \to \omega = \frac{{2\pi }}{T} = \pi ({\rm{rad}}/{\rm{s}})\)

Góc quét \(\omega \Delta t = 0,25\pi \Rightarrow x = - \frac{{A\sqrt 2 }}{2} = - 5\sqrt 2 \;{\rm{cm}}\)

\(a = - {\omega ^2}x = 5\sqrt 2 {\pi ^2}\;{\rm{cm}}/{{\rm{s}}^2}\)