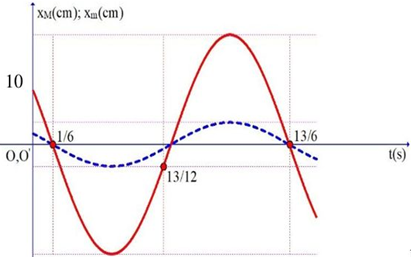
Một con lắc lò xo dao động trên phương ngang không ma sát, vật nặng có khối lượng \(m\), lò xo có độ cứng \(k\), trên lò xo có một điểm \(M\). Khi vật m dao động điều hòa quanh vị trí cân bằng \(O\) thì \(M\) trên lò xo cũng dao động quanh vị trí cân bằng O’. Đồ thị sự phụ thuộc của li độ theo thời gian của \(m\) và \(M\) quanh \(O\) và \(O\)' như hình vẽ. Tại thời điểm \(t = \frac{2}{3}\;s\) thì điểm \(M\) được giữ cố định, khi đó vật \(m\) sẽ dao động với biên độ gần nhất với giá trị nào sau đây?

D. \(17\;cm\).

Đáp án: A

 \[T = \frac{{13}}{6} - \frac{1}{6} = 2s \to \omega = \frac{{2\pi }}{T} = \pi ({\rm{rad}}/{\rm{s}})\]

\[{x_m} = {A_m}\cos \left[ {\pi \left( {t - \frac{1}{6}} \right) + \frac{\pi }{2}} \right] = {A_m}\cos \left( {\pi t + \frac{\pi }{3}} \right)\]

Tại t = 0 thì \[10 = {A_m}\cos \left( {\pi \cdot 0 + \frac{\pi }{3}} \right) \Rightarrow {A_m} = 20\;{\rm{cm}}\]

Tại \[t = \frac{{13}}{{12}}s\] thì -\[{A_M} = 20\cos \left( {\pi \cdot \frac{{13}}{{12}} + \frac{\pi }{3}} \right)\]\[ \Rightarrow {A_M} = 5\sqrt 6 - 5\sqrt 2 \;{\rm{cm}}\]

Tại \[t = \frac{2}{3}s\] thì \[{x_m} = {A_m}\cos \left( {\pi \frac{2}{3} + \frac{\pi }{3}} \right) = - {A_m} \Rightarrow {x_M} = - {A_M}\](M cùng pha với m)

Giữ cố định điểm M thì vị trí cân bằng dịch sang trái một đoạn bằng \(\left| {{x_M}} \right| = {A_M}\)

Biên độ của vật m lúc sau là \({A_m} - {A_M} = 20 - (5\sqrt 6 - 5\sqrt 2 ) \approx 14,824\;{\rm{cm}}\)