Một vật dao động điều hoà với chu kì T. Tại thời điểm ban đầu, vật đi qua vị trí
Một vật dao động điều hoà với chu kì T. Tại thời điểm ban đầu, vật đi qua vị trí cân bằng. Tính tỉ số giữa động năng và thế năng của vật vào thời điểm T12.
Một vật dao động điều hoà với chu kì T. Tại thời điểm ban đầu, vật đi qua vị trí cân bằng. Tính tỉ số giữa động năng và thế năng của vật vào thời điểm T12.
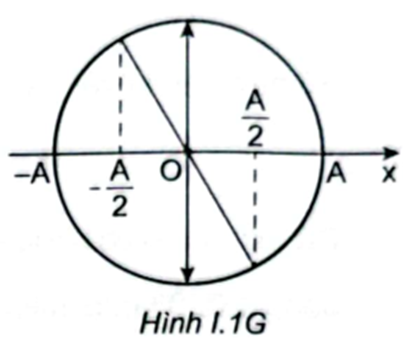
Theo giản đồ Hình I.2G, ta thấy khi t=T12 thì x=±A2
Wt=12kx2=12k(A2)2=14kA22=14W
Wd=W−Wt=W−14W=34W⇒WdWt=3.