Một vật dao động điều hoà dọc theo trục \({\rm{Ox}}\) nằm ngang, gốc \({\rm{O}}\) và mốc thế năng ở vị trí cân bằng. Cứ sau \(0,5{\rm{\;s}}\) thì động năng lại bằng thế năng và vật đi được đoạn đường dài nhất trong thời gian \(0,5{\rm{\;s}}\) là \(4\sqrt 2 {\rm{\;cm}}\). Chọn \({\rm{t}} = 0\) là lúc vật qua vị trí cân bằng theo chiều dương. Viết phương trình dao động của vật.

Khi \({W_t} = {W_d} \Rightarrow {W_t} = \frac{W}{2}\)\( \Leftrightarrow \frac{{k{x^2}}}{2} = \frac{1}{2}\frac{{k{A^2}}}{2} \Rightarrow x = \pm \frac{{A\sqrt 2 }}{2}\)

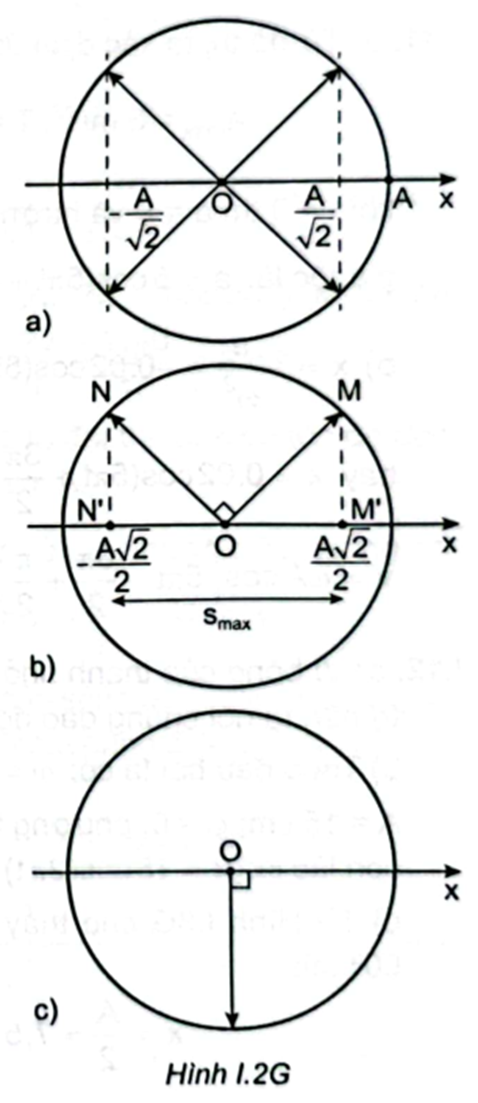
Từ giản đồ ở Hình I.2Ga, ta có: \(\frac{T}{4} = 0,5 \Rightarrow T = 4.0,5 = 2\;{\rm{s}}\)\( \Rightarrow \omega = \frac{{2\pi }}{T} = \pi {\rm{(rad/s)}}\)

Từ giản đồ Hình I.2Gb, ta có: \({{\rm{S}}_{\max }} = A\sqrt 2 = 4\sqrt 2 \;{\rm{cm}}\)\( \Rightarrow A = 4\;{\rm{cm}}\).

Vì \({\rm{t}} = 0\) lúc vật qua vị trí cân bằng theo chiều dương \( \Rightarrow \) pha ban đầu là:\(\varphi = - \frac{\pi }{2}\)(Hình I.2Gb)

Vậy phương trình dao động của vật là: \(x = 4\cos \left( {\pi t - \frac{\pi }{2}} \right)({\rm{cm}}).\)