Câu hỏi:
03/04/2024 37
Một túi đựng 9 quả cầu màu xanh, 3 quả cầu màu đỏ, 7 quả cầu màu vàng. Lấy ngẫu nhiên 6 quả cầu trong túi. Tính xác suất sao cho lấy được cả ba loại cầu, đồng thời số quả cầu màu xanh bằng số quả cầu màu đỏ.
A. \(\frac{{165}}{{1292}}\)
B. \(\frac{9}{{76}}\)
C. \(\frac{{118}}{{969}}\)
D. \(\frac{{157}}{{1292}}\)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
- Tính số phần tử của không gian mẫu (số cách chọn 6 trong 19 quả cầu).
- Liệt kê và đếm số cách lấy mà số quả cầu xanh bằng số quả cầu đỏ.
- Tính xác suất theo công thức \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
Cách giải:
Số cách chọn 6 trong 19 quả cầu là \(n\left( \Omega \right) = C_{19}^6\)
Gọi A là biến cố: Lấy được 6 quả cầu đủ ba loại sao cho số quả cầu xanh bằng số quả cầu đỏ. Ta đếm số cách chọn 6 quả cầu đủ ba loại sao cho số quả cầu xanh bằng số quả cầu đỏ.
+ TH1: 1 quả xanh, 1 quả đỏ và 4 quả vàng có \(C_9^1.C_3^1.C_7^4\) cách chọn.
+ TH2: 2 quả xanh, 2 quả đỏ và 2 quả vàng có \(C_9^2.C_3^2.C_7^2\) cách chọn.
Suy ra \(n\left( A \right) = C_9^1.C_3^1.C_7^4 + C_9^2.C_3^2.C_7^2\)
Vậy xác suất là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_9^1.C_3^1.C_7^4 + C_9^2.C_3^2.C_7^2}}{{C_{19}^6}} = \frac{9}{{76}}\)
Đáp án B
Phương pháp:
- Tính số phần tử của không gian mẫu (số cách chọn 6 trong 19 quả cầu).
- Liệt kê và đếm số cách lấy mà số quả cầu xanh bằng số quả cầu đỏ.
- Tính xác suất theo công thức \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
Cách giải:
Số cách chọn 6 trong 19 quả cầu là \(n\left( \Omega \right) = C_{19}^6\)
Gọi A là biến cố: Lấy được 6 quả cầu đủ ba loại sao cho số quả cầu xanh bằng số quả cầu đỏ. Ta đếm số cách chọn 6 quả cầu đủ ba loại sao cho số quả cầu xanh bằng số quả cầu đỏ.
+ TH1: 1 quả xanh, 1 quả đỏ và 4 quả vàng có \(C_9^1.C_3^1.C_7^4\) cách chọn.
+ TH2: 2 quả xanh, 2 quả đỏ và 2 quả vàng có \(C_9^2.C_3^2.C_7^2\) cách chọn.
Suy ra \(n\left( A \right) = C_9^1.C_3^1.C_7^4 + C_9^2.C_3^2.C_7^2\)
Vậy xác suất là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_9^1.C_3^1.C_7^4 + C_9^2.C_3^2.C_7^2}}{{C_{19}^6}} = \frac{9}{{76}}\)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Giải bóng đá Vô địch quốc gia Việt Nam 2018 (Nuti Café V.League 2018) có 14 đội bóng tham dự theo thể thức vòng tròn tính điểm lượt đi - lượt về (nghĩa là 2 đội bất kì sẽ đấu với nhau đúng 2 trận). Hỏi có tất cả bao nhiêu trận đấu diễn ra trong cả giải đấu đó?
Câu 2:
Trong một trò chơi, người chơi cần gieo cùng lúc ba con súc sắc cân đối, đồng chất; nếu được ít nhất hai con súc sắc xuất hiện mặt có số chấm lớn hơn 4 thì người chơi đó thắng. Tính xác suất để trong ba lần chơi, người chơi thắng ít nhất một lần.
Câu 3:
Gieo đồng thời hai con súc sắc (khác nhau, cân đối, đồng chất). Xác suất tổng số chấm xuất hiện trên hai súc sắc bằng 7 là
Câu 4:
Có bao nhiêu cách xếp ba bạn nam và hai bạn nữ thành một hàng ngang sao cho hai bạn nữ không đứng cạnh nhau?
Câu 5:
Khai triển biểu thức \(P\left( x \right) = {\left( {2x + 1} \right)^{17}}\) thu được bao nhiêu số hạng?
Câu 6:
Cho tam giác ABC có trọng tâm G. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Phép vị tự nào sau đây biến tam giác ABC thành tam giác MNP?
Câu 7:
Trong không gian cho các đường thẳng \(a,\,b\) và các mặt phẳng \(\left( \alpha \right),\,\left( \beta \right)\). Trong các khẳng định sau đây, đâu là khẳng định đúng?
Câu 8:
Tập nghiệm của phương trình \(\cos 2x - \sin x = 0\) được biểu diễn bởi tất cả bao nhiêu điểm trên đường tròn lượng giác?
Câu 9:
Trong một hộp có 9 tấm thẻ được đánh số từ 1 đến 9. Lấy ngẫu nhiên ra bốn thẻ và xếp cạnh nhau theo thứ tự từ trái sang phải. Tính xác suất để bốn thẻ đó xếp thành một số tự nhiên chẵn.
Câu 10:
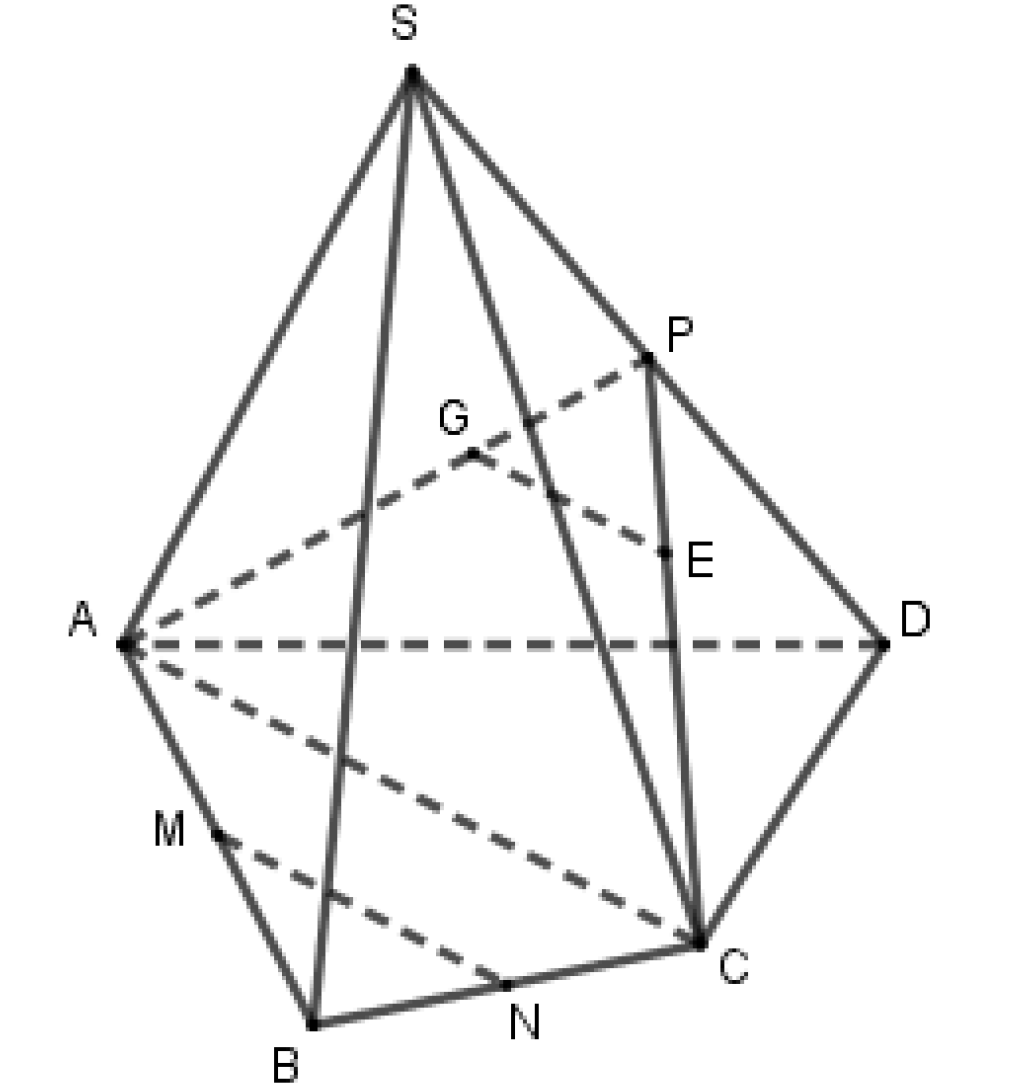
Cho hình chóp \(S.ABCD\). Gọi G, E lần lượt là trọng tâm các tam giác SAD và SCD. Lấy M, N lần lượt là trung điểm AB, BC. Khẳng định nào sau đây đúng?

Câu 11:
Một đội công nhân trồng cây xanh trên đoạn đường dài 5,27 kilomet. Cứ 50 mét trồng một cây. Hỏi có bao nhiêu cây được đội công nhân trồng trên đoạn đó (cây đầu tiên được trồng ở ngay đầu đoạn đường)?
Câu 12:
Cho lăng trụ \(ABCD.A'B'C'D'\) có hai đáy là các hình bình hành. Các điểm M, N, P lần lượt là trung điểm của cạnh AD, BC, CC' (tham khảo hình vẽ). Xét các khẳng định sau:
I) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(A'D'\)
II) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại trung điểm của \(DD'\)
III) Mặt phẳng \(\left( {MNP} \right)\) song song với mặt phẳng \(\left( {ABC'D'} \right)\)
Trong các khẳng định trên, số khẳng định đúng là
Cho lăng trụ \(ABCD.A'B'C'D'\) có hai đáy là các hình bình hành. Các điểm M, N, P lần lượt là trung điểm của cạnh AD, BC, CC' (tham khảo hình vẽ). Xét các khẳng định sau:
I) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(A'D'\)
II) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại trung điểm của \(DD'\)
III) Mặt phẳng \(\left( {MNP} \right)\) song song với mặt phẳng \(\left( {ABC'D'} \right)\)
Trong các khẳng định trên, số khẳng định đúng là
Câu 13:
Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?
I) Hàm số \(y = x + {\mathop{\rm sinx}\nolimits} \) tuần hoàn với chu kì \(T = 2\pi \)
II) Hàm số \(y = x\cos x\) là hàm số lẻ
III) Hàm số \(y = \tan x\) đồng biến trên từng khoảng xác định
Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?
I) Hàm số \(y = x + {\mathop{\rm sinx}\nolimits} \) tuần hoàn với chu kì \(T = 2\pi \)
II) Hàm số \(y = x\cos x\) là hàm số lẻ
III) Hàm số \(y = \tan x\) đồng biến trên từng khoảng xác định


