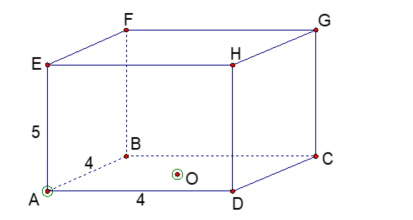
Một chiếc hộp hình hộp chữ nhật ABCD.FEGH, mặt trên EFGH không có nắp (xem hình bên).

Một chiếc hộp hình hộp chữ nhật ABCD.FEGH, mặt trên EFGH không có nắp (xem hình bên).

Có một con kiến ở đỉnh A bên ngoài hộp và một miếng mồi của kiến tại điểm O là tâm đáy ABCD ở bên trong hộp. Tính quãng đường ngắn nhất mà con kiến tìm đến miếng mồi (làm tròn đến một chữ số thập phân).

Trả lời

Chọn C.

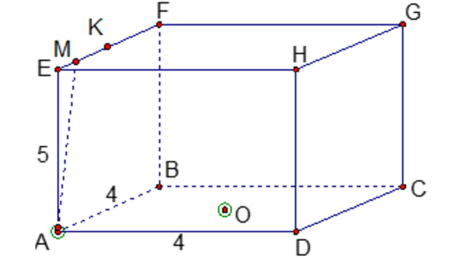
                       ( Hình 1)                                                   

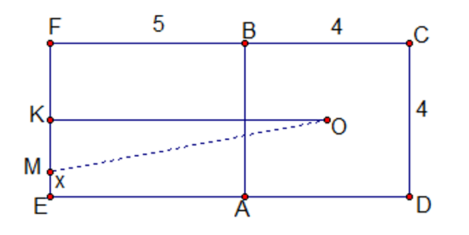
  ( Hình 2)

Đầu tiên kiến bò đến điểm M trên miệng hộp ( M thuộc đoạn EK với K là trung điểm EF )

( cạnh EF và EH là như nhau – với mỗi điểm M thuộc đoạn EK, có điểm M* thuộc đoạn KF sao cho MO = M*O ). Tiếp tục kiến thực hiện quãng đường ngắn nhất ( bên trong hộp ) từ M đến O- lúc này ta trải hai hình chữ nhật EFBA và ABCD lên mặt phẳng.  

Gọi EM =x, 0 $\le$ x $\le$ 2 và S là quãng đường ( ngắn nhất)  mà kiến thực hiện.

S = AM +MO

Trên hình 1 thì $AM=\sqrt{A{E}^2+E{M}^2}$, trên hình 2 ( hình khai triển) thì MO = $\sqrt{O{K}^2+K{M}^2}$

Ta có:

$S=\sqrt{A{E}^2+E{M}^2}+\sqrt{O{K}^2+K{M}^2}=\sqrt{5^2+x^2}+\sqrt{7^2+{(2-x)}^2}\ge \sqrt{{(5+7)}^2+{(x+2-x)}^2}=12,17$ 

( chú ý $\sqrt{5^2+x^2}+\sqrt{7^2+{(2-x)}^2}\ge \sqrt{{(5+7)}^2+{(x+2-x)}^2}$ là bất đẳng thức $\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|\ge |\overrightarrow{a}+\overrightarrow{b}|$

Dấu = xảy ra khi $\frac{5}{7}=\frac{x}{2-x}\Rightarrow x=\frac{5}{6}$.