Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích

Bài 5.8 trang 82 Toán 10 Tập 1: Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích và tính giá trị của số đặc trưng đó.

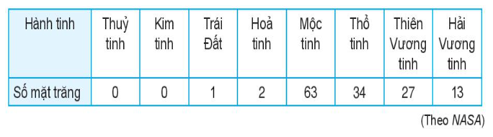
a) Số mặt trăng đã biết của các hành tinh:

b) Số đường chuyền thành công trong một trận đấu của một số cầu thủ bóng đá:

32   24   20   14   23.

c) Chỉ số IQ của một nhóm học sinh:

80   102   83   103   108   94   110   106   104   100.

d) Các sai số trong một phép đo:

10   15   18   15   14   13   42   15   12   14   42.

Trả lời

a) Sắp xếp lại số liệu:

0   0   1   2   13   27   34   63

Mẫu số liệu đã cho có số liệu tăng dần, do đó ta nên dùng số trung bình để đo xu thế trung tâm của mẫu số liệu này.

Số trung bình của mẫu số liệu là:

$\overline{x}=\frac{0+0+1+2+13+27+34+63}{8}=17,5$.

Ta không dùng trung vị vì M_e = (2 + 13) : 2 = 7,5, giá trị này chênh lệch nhiều so với các số liệu ở nửa bên phải.

b) Các số liệu bài cho không chênh lệch quá lớn với nhau nên ta chọn số trung bình làm số đặc trưng đo xu thế trung tâm.

Số đường chuyền trung bình là:

$\frac{32+24+20+14+23}{5}=22,6$.

c) Các số liệu bài cho không chênh lệch quá lớn với nhau nên ta chọn số trung bình làm số đặc trưng đo xu thế trung tâm.

Chỉ số IQ trung bình của nhóm học sinh là:

$\frac{80+102+83+103+108+94+110+106+104+100}{10}=99.$

d) Mẫu số liệu đã cho có đa số các sai số là giống nhau, riêng giá trị 42 lớn hơn hẳn các giá trị khác, đây được xem là giá trị bất thường nên ta chọn số trung vị là số đặc trưng đo xu thế trung tâm của mẫu số liệu đã cho.

Sắp xếp dãy số liệu đã cho theo thứ tự không giảm ta được:

10; 12; 13; 14; 14; 15; 15; 15; 18; 42; 42

Vì dãy số liệu có 11 số nên trung vị của mẫu là M_e = 15.

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

Bài 13: Các số đặc trưng đo xu thế trung tâm

Bài 14: Các số đặc trưng. Đo độ phân tán

Bài tập cuối chương 5

Tìm hiểu một số kiến thức về tài chính