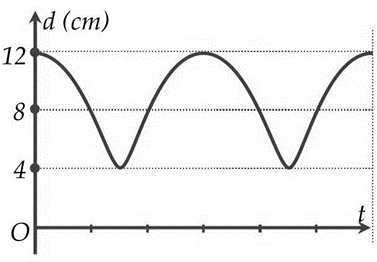
Hai vật nhỏ dao động điều hòa cùng tần số góc \(10{\rm{rad}}/{\rm{s}}\), cùng biên độ trên hai đường thẳng vuông góc với nhau tại vị trí cân bằng chung \({\rm{O}}\). Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của khoảng cách (d) giữa hai vật theo thời gian. Tại thời điểm mà gia tốc của một trong hai vật bị triệt tiêu thì vật còn lại có tốc độ bằng bao nhiêu?

D. \(78,38{\rm{\;cm}}/{\rm{s}}\)

\[{d^2} = x_1^2 + x_2^2 = {A^2}\left[ {{{\cos }^2}\left( {\omega t} \right) + {{\cos }^2}\left( {\omega t + \varphi } \right)} \right] = \]

\[ = {A^2}\left[ {\frac{{2 + \cos \left( {2\omega t} \right) + \cos \left( {2\omega t + 2\varphi } \right)}}{2}} \right] = {A^2}\left[ {1 + \cos \varphi \cos \left( {2\omega t + \varphi } \right)} \right]\]

\( \Rightarrow \left\{ \begin{array}{l}d_{\max }^2 = {A^2}\left( {1 + \left| {\cos \varphi } \right|} \right) = {12^2}\\d_{\min }^2 = {A^2}\left( {1 - \left| {\cos \varphi } \right|} \right) = {4^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left| {\cos \varphi } \right| = 0,8\\A = 4\sqrt 5 cm\end{array} \right.\)

\({v_{\max }} = \omega A = 10.4\sqrt 5 = 40\sqrt 5 \) (cm/s)

Khi một vật có \(a = 0 \Rightarrow v = {v_{\max }}\) thì vật còn lại có \(v = {v_{\max }}\left| {\cos \varphi } \right| = 40\sqrt 5 .0,8 \approx 71,55cm/s\). Chọn A