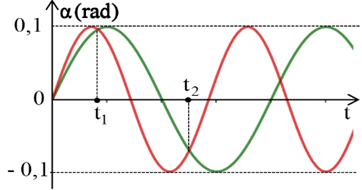
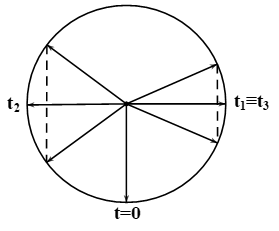
Hai con lắc đơn có chiều dài ${\ell _1} = \,100\,{\rm{cm}}$ và ${\ell _2}$ (với ${\ell _2} < {\ell _1})$ được treo tại cùng một nơi có ${\rm{g = 10}}\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}.$Bỏ qua lực cản không khí, lấy ${{\rm{\pi }}^{\rm{2}}} = 10.$ Ban đầu, từ vị trí cân bằng đồng thời truyền vận tốc ban đầu nằm ngang, cùng chiều cho mỗi con lắc sao cho chúng dao động điều hòa cùng trong hai mặt phẳng song song với nhau. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của li độ góc của mỗi con lắc theo thời gian. Biết ${{\rm{t}}_{\rm{2}}}{\rm{ - }}{{\rm{t}}_{\rm{1}}}{\rm{ = }}\frac{{\rm{8}}}{{\rm{9}}}\,{\rm{s}}{\rm{.}}$ Không kể lúc truyền vận tốc, tại thời điểm mà hai dây treo song song với nhau lần thứ 2023 thì tốc độ của con lắc có chiều dài ${\ell _2}$là

D. $14,0\,{\rm{cm/s}}{\rm{.}}$

${\omega _1} = \sqrt {\frac{g}{{{l_1}}}} \approx \sqrt {\frac{{{\pi ^2}}}{1}} = \pi$ (rad/s) $\Rightarrow {T_1} = \frac{{2\pi }}{{{\omega _1}}} = 2s$ và ${l_2} < {l_1} \Rightarrow {\omega _2} > {\omega _1}$

(chú ý nghiệm ${\omega _2}t = {\omega _1}t + k2\pi$ là cùng chiều, còn nghiệm ${\omega _2}t = \pi - {\omega _1}t + h2\pi$ là ngược chiều)

 (rad/s) $\Rightarrow \left\{ \begin{array}{l}{T_2} = \frac{{2\pi }}{{{\omega _2}}} = 1,6s\\{l_2} = \frac{g}{{\omega _2^2}} = 0,64m\end{array} \right.$

$\frac{{{T_1}}}{{{T_2}}} = \frac{2}{{1,6}} = \frac{5}{4} \Rightarrow {T_{12}} = 8s$ thì 2 vật lặp lại trạng thái ban đầu nên ta chỉ cần xét trong 8s đầu

Từ cứ ${T_{12}} = 8s$ thì có 10 lần

$2013 = 201.10 + 3 \Rightarrow {t_3} = \frac{4}{9} + \frac{{8.2}}{9} = \frac{{20}}{9}s$

${s_2} = {l_2}{\alpha _2} = {l_2}{\alpha _0}\sin \left( {{\omega _2}t} \right) \Rightarrow {v_2} = {s_2}' = {l_2}{\alpha _0}{\omega _2}\cos \left( {{\omega _2}t} \right) = 0,64.0,1.\frac{{5\pi }}{4}.\cos \left( {\frac{{5\pi }}{4}.\frac{{20}}{9}} \right) \approx - 0,193m/s$Vậy $\left| {{v_2}} \right| \approx 19,3cm/s$. Chọn A

Cách 2:

${\omega _1} = \sqrt {\frac{g}{{{l_1}}}} \approx \sqrt {\frac{{{\pi ^2}}}{1}} = \pi$ (rad/s) $\Rightarrow {T_1} = \frac{{2\pi }}{{{\omega _1}}} = 2s$

Tạo dao động ảo có tần số góc $\omega = \frac{{{\omega _1} + {\omega _2}}}{2} \Rightarrow$pha dao động cũng bằng trung bình cộng

$\Rightarrow {t_2} - {t_1} = \frac{T}{2} = \frac{8}{9}s \Rightarrow T = \frac{{16}}{9}s \Rightarrow \omega = \frac{{2\pi }}{T} = \frac{{9\pi }}{8} = \frac{{\pi + {\omega _2}}}{2} \Rightarrow {\omega _2} = \frac{{5\pi }}{4}(rad/s) \Rightarrow \left\{ \begin{array}{l}{T_2} = \frac{{2\pi }}{{{\omega _2}}} = 1,6s\\{l_2} = \frac{g}{{\omega _2^2}} = 0,64m\end{array} \right.$$\frac{{{T_1}}}{{{T_2}}} = \frac{2}{{1,6}} = \frac{5}{4} \Rightarrow$ cứ ${T_{12}} = 8s$ thì hơn nhau 1 dao động nên cứ sau $8s$ mới có 1 lần 2 dao động cùng pha mà ${T_{12}} = 8s = \frac{T}{4} + 8,5.\frac{T}{2} \Rightarrow$có 9 lần dao động ảo đi qua biên + 1 lần cùng pha: 10 lần

$2013 = 201.10 + 3 \Rightarrow {t_3} = \frac{T}{4} + 2.\frac{T}{2} = \frac{{20}}{9}s$

${s_2} = {l_2}{\alpha _2} = {l_2}{\alpha _0}\cos \left( {{\omega _2}t - \frac{\pi }{2}} \right) \Rightarrow {v_2} = {l_2}{\alpha _0}{\omega _2}\cos \left( {{\omega _2}t} \right) = 0,64.0,1.\frac{{5\pi }}{4}.\cos \left( {\frac{{5\pi }}{4}.\frac{{20}}{9}} \right) \approx - 0,193m/s$Vậy $\left| {{v_2}} \right| \approx 19,3cm/s$. Chọn A