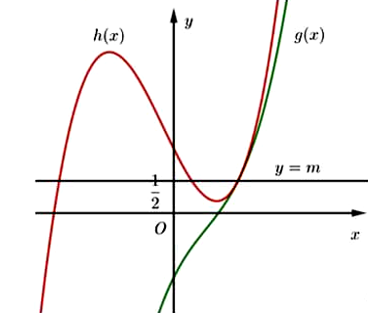
Ta có giao điểm của đồ thị h(x) và g(x) là điểm $K\left(1;\frac{1}{2}\right)$

Ta có $h\text{'}\left(x\right)=3x^2-3x+2>0,\forall x\in ℝ\Rightarrow h\left(x\right)$ đồng biến trên $\mathrm{ℝ}$.

Ta có: $g\text{'}\left(x\right)=3x^2+x-2=0\iff \left[\begin{array}{l}x=-1\\ x=\frac{2}{3}\end{array}\right.$

Điểm cực đại của đồ thị $H\left(-1;\frac{5}{2}\right)$, điểm cực tiểu của đồ thị $L\left(\frac{2}{3};\frac{5}{27}\right)$

Như vậy để phương trình đã cho có đúng 3 nghiệm thì (**) có đúng 3 nghiệm $\iff$ pt (1) có 1 nghiệm và pt (2) có đúng 2 nghiệm phân biệt hoặc pt (1) có 1 nghiệm và pt (2) có đúng 3 nghiệm phân biệt trong đó có 1 nghiệm chung $x=1$

$\iff m=\frac{5}{2}\vee m=\frac{5}{27}\vee m=\frac{1}{2}$ suy ra tích các giá trị m thỏa yêu cầu bài toán là $\frac{25}{108}.$