Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB

Bài 9.26 trang 81 Toán 7 Tập 2:

Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB.

Trả lời

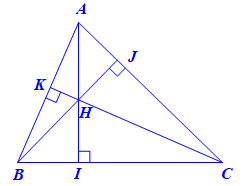
Gọi I, J, K lần lượt là chân đường cao kẻ từ A, B, C đến BC, CA, AB.

Xét DHBC có HI ⊥ BC, CJ ⊥ BH.

Mà HI cắt CJ tại A nên A là trực tâm của $∆$HBC.

Xét $∆$HCA có HJ ⊥ AC, CI ⊥ AH.

Mà HJ cắt CI tại B nên B là trực tâm của $∆$HCA.

Xét $∆$HAB có HK ⊥ AB, BI ⊥ AH.

Mà HK cắt BI tại C nên C là trực tâm của $∆$HAB.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 33: Quan hệ giữa ba cạnh của một tam giác

Luyện tập chung trang 71

Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác

Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Luyện tập chung trang 83

Bài tập cuối chương 9