Cho tam giác ABC có góc A = 100 độ và trực tâm H. Tính góc BHC

Bài 9.27 trang 81 Toán 7 Tập 2:

Cho tam giác ABC có $\widehat{A}$ = 100^o và trực tâm H. Tính góc BHC.

Trả lời

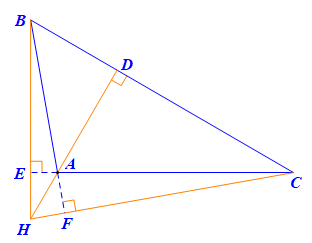
Gọi D, E, F lần lượt là chân đường cao kẻ từ A, B, C đến BC, CA, AB.

Ta có $\widehat{BA\text{D}}=\widehat{F\text{A}H}$ (2 góc đối đỉnh), $\widehat{DAC}=\widehat{EAH}$ (2 góc đối đỉnh).

Do đó $\widehat{BA\text{D}}+\widehat{DAC}=\widehat{F\text{AH}}+\widehat{EAH}$ = 100°.

Xét $∆$FAH vuông tại F có $\widehat{FHA}+\widehat{F\text{A}H}$ = 90° (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $\widehat{FHA}=90°-\widehat{F\text{A}H}$.

Xét $∆$EAH vuông tại E: $\widehat{EHA}+\widehat{\text{EA}H}$ = 90° (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $\widehat{EHA}=90°-\widehat{\text{EA}H}$.

Khi đó $\widehat{FHA}+\widehat{EHA}=90°-\widehat{F\text{A}H}+90°-\widehat{E\text{A}H}$

Hay $\widehat{BHC}=180°-\left(\widehat{F\text{A}H}+\widehat{E\text{AH}}\right)$.

Do đó $\widehat{BHC}$ = 180° - 100° = 80°.

Vậy $\widehat{BHC}$ = 80°.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 33: Quan hệ giữa ba cạnh của một tam giác

Luyện tập chung trang 71

Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác

Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Luyện tập chung trang 83

Bài tập cuối chương 9