Gọi A’, B’ và C’ lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép vị tự V(O, k). Cho biết
Gọi A’, B’ và C’ lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép vị tự V(O, k). Cho biết →BA=m→BC, hai vectơ B' và có bằng nhau không?
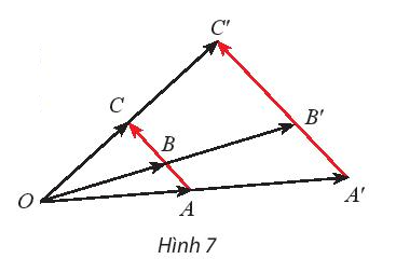
Gọi A’, B’ và C’ lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép vị tự V(O, k). Cho biết →BA=m→BC, hai vectơ B' và có bằng nhau không?

Theo bài, ta có A’, B’ lần lượt là ảnh của A, B qua V(O, k).
Áp dụng tính chất 1, ta được .
Chứng minh tương tự, ta được .
Ta có .
Vậy hai vectơ và bằng nhau.