Giải các phương trình sau: a) căn ( x^2 -7x) = căn ( -9x^2 - 8x + 3 )
Bài 4 trang 18 Toán lớp 10 Tập 2: Giải các phương trình sau:
a) √x2−7x=√−9x2−8x+3;
b) √x2+x+8−√x2+4x+1=0;
c) √4x2+x−1=x+1;
d) √2x2−10x−29=√x−8.
Bài 4 trang 18 Toán lớp 10 Tập 2: Giải các phương trình sau:
a) √x2−7x=√−9x2−8x+3;
b) √x2+x+8−√x2+4x+1=0;
c) √4x2+x−1=x+1;
d) √2x2−10x−29=√x−8.
a) √x2−7x=√−9x2−8x+3
⇒ x2 – 7x = - 9x2 – 8x + 3
⇒ 10x2 + x – 3 = 0
⇒ x = 12 và x = −35
Thay lần lượt hai giá trị vào phương trình đã cho ta thấy chỉ có giá trị x = −35 thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là 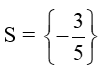
b) √x2+x+8−√x2+4x+1=0
⇒ √x2+x+8=√x2+4x+1
⇒ x2 + x + 8 = x2 + 4x + 1
⇒ 3x = 7
⇒ x = 73
Thay x = 73 vào phương trình đã cho ta thấy thỏa mãn.
Vậy tập nghiệm của phương trình là 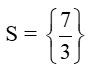
c) √4x2+x−1=x+1
⇒ 4x2 + x – 1 = x2 + 2x + 1
⇒ 3x2 – x – 2 = 0
⇒ x = 1 và x = −23
Thay lần lượt các giá trị của x vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.
Vậy tập nghiệm của phương trình là 
d) √2x2−10x−29=√x−8
⇒ 2x2 – 10x – 29 = x – 8
⇒ 2x2 – 11x – 21 = 0
⇒ x = 7 và x = −32
Thay lần lượt hai giá trị này vào phương trình đã cho ta thấy cả hai giá trị đều không thỏa mãn.
Vậy tập nghiệm của phương trình là S = ∅ .
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Giải bất phương trình bậc hai một ẩn
Bài 3: Phương trình quy về phương trình bậc hai
Bài 1: Quy tắc cộng và quy tắc nhân