Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây
1.4k
13/06/2023
Bài 1 trang 12 Toán lớp 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:
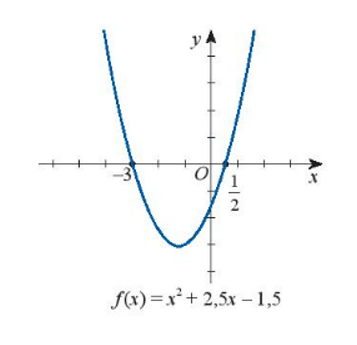
a) x2 + 2,5x – 1,5 ≤ 0;
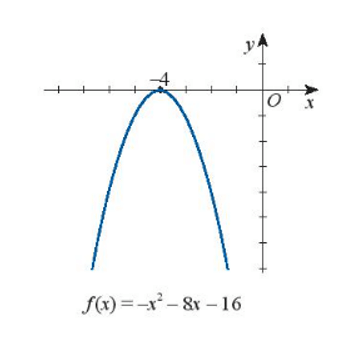
b) – x2 – 8x – 16 < 0
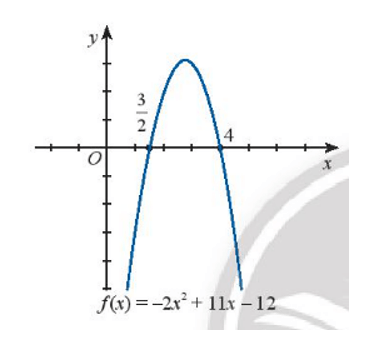
c) – 2x2 + 11x – 12 > 0
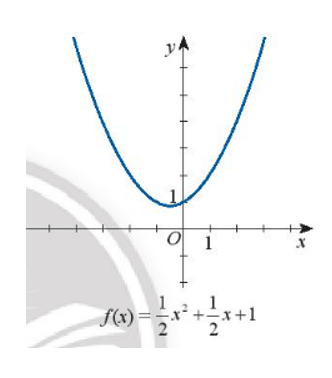
d) 12 x2 + 12 x + 1 ≤ 0
Trả lời
a)

Dựa vào hình vẽ ta thấy:
Đồ thị hàm số f(x) cắt trục hoành tại hai điểm có hoành độ lần lượt là x1 = -3 và x2 = 12 hay với x1 = -3 và x2 = 12 thì f(x) = 0.
Trong hai khoảng (-∞; - 3) và (12;+∞) đồ thị hàm số f(x) nằm phía trên trục hoành hay f(x) > 0 khi x thuộc hai khoảng (-∞; - 3) và (12;+∞) .
Trong khoảng (−3;12) đồ thị hàm số f(x) nằm phía dưới trục hoành hay f(x) < 0 khi x thuộc khoảng (−3;12) .
Vậy bất phương trình x2 + 2,5x – 1,5 ≤ 0 có tập nghiệm là 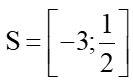 .
.
b)

Dựa vào hình vẽ ta thấy:
Đồ thị hàm số f(x) cắt trục hoành tại một điểm có hoành độ x = -4 hay f(x) = 0 khi x = -4.
Với x ≠ -4 thì đồ thị hàm số f(x) nằm phía dưới trục hoành nên f(x) < 0 với x ≠ -4.
Vậy bất phương trình – x2 – 8x – 16 < 0 có tập nghiệm là S = ℝ\{-4}.
c)

Dựa vào hình vẽ ta thấy:
Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt x1 = 32 và x2 = 4 hay f(x) = 0 khi x1 = 32 và x2 = 4.
Đồ thị hàm số f(x) nằm phía dưới trục hoành với x thuộc hai khoảng (−∞;32) và (4; +∞) hay f(x) < 0 với x thuộc (−∞;32) ∪ (4; +∞).
Đồ thị hàm số f(x) nằm phía trên trục hoành với x thuộc khoảng (32;4) hay f(x) > 0 với x thuộc khoảng (32;4) .
Vậy bất phương trình – 2x2 + 11x – 12 > 0 có tập nghiệm S = (32;4) .
d)

Dựa vào hình vẽ ta thấy:
Đồ thi hàm số f(x) nằm phía trên trục hoành với mọi x hay f(x) > 0 với x ∈ ℝ.
Vậy bất phương trình 12x2 + 12x + 1 ≤ 0 có tập nghiệm S = ∅.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Dùng bảng tính để tính các số đặc trưng của mẫu số liệu thống kê
Bài 1: Dấu của tam thức bậc hai
Bài 2: Giải bất phương trình bậc hai một ẩn
Bài 3: Phương trình quy về phương trình bậc hai
Bài tập cuối chương 7
Bài 1: Quy tắc cộng và quy tắc nhân





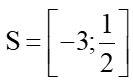 .
.