Có bao nhiêu giá trị nguyên của tham số m (với |m| < 2021)

Có bao nhiêu giá trị nguyên của tham số m (với $\left|m\right|<2021$) để phương trình $2^{x-1}={\log }_4\left(x+2m\right)+m$ có nghiệm?

Trả lời

Chọn A

Ta có $2^{x-1}={\log }_4\left(x+2m\right)+m\iff 2^x={\log }_2\left(x+2m\right)+2m$.

Đặt $a={\log }_2\left(x+2m\right)\Rightarrow 2m=2^a-x$, phương trình đã cho trở thành

$2^x=a+2^a-x\iff 2^x+x=2^a+a$ (1)

Xét hàm số $f\left(t\right)=2^t+t$, có $f^{\text{'}}\left(t\right)=2^t\ln 2+1>0,\forall t\in ℝ$ suy ra f(t) đồng biến trên R.

Khi đó $\left(1\right)\iff f\left(x\right)=f\left(a\right)\iff x=a$, suy ra $x={\log }_2\left(x+2m\right)\iff 2m=2^x-x$ (2)

Xét hàm số $g\left(x\right)=2^x-x$, ta có $g^{\text{'}}\left(x\right)=2^x\ln 2-1$

$\Rightarrow g^{\text{'}}\left(x\right)=0\iff 2^x\ln 2-1=0\iff x=-{\log }_2\ln 2=x_0$

Bảng biến thiên

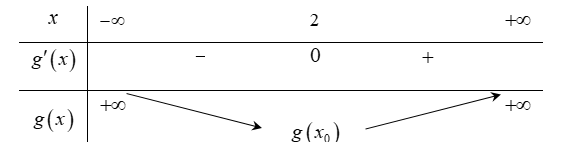
Do đó (2) có nghiệm khi và chỉ khi $2m\ge g\left(x_0\right)=\frac{1}{\ln 2}+{\log }_2\ln 2\iff m\ge \frac{1}{2\ln 2}+\frac{1}{2}{\log }_2\ln 2\approx 0,46$

Do $\left|m\right|<2021,m\in \mathbb{Z}$ nên $m\in \left\{1;2;\mathrm{...};2020\right\}$, do đó có 2020 giá trị nguyên của m thỏa mãn đề bài.