Câu hỏi:
03/04/2024 56
Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc quay α(α≠k2π,k∈ℤ).
A. 2
B. Vô số
C. 1
D. 0
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Có duy nhất điểm O biến thành chính nó qua phép quay tâm O góc quay α(α≠k2π,k∈ℤ).
Chọn C
Có duy nhất điểm O biến thành chính nó qua phép quay tâm O góc quay α(α≠k2π,k∈ℤ).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tổng các nghiệm của phương trình tan2x=tan(π4−x) trên nửa khoảng [0;2π) bằng
Tổng các nghiệm của phương trình tan2x=tan(π4−x) trên nửa khoảng [0;2π) bằng
Câu 2:
Cho hình chóp SABCD có AB và CD không song song. Gọi O là giao điểm của AC và BD. Cho M là một điểm thuộc miền trong của tam giác SCD. Khẳng định nào sau đây sai?
Cho hình chóp SABCD có AB và CD không song song. Gọi O là giao điểm của AC và BD. Cho M là một điểm thuộc miền trong của tam giác SCD. Khẳng định nào sau đây sai?
Câu 3:
Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức h=−3cos(πt12+π6)+12. Mực nước của kênh cao nhất khi
Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức h=−3cos(πt12+π6)+12. Mực nước của kênh cao nhất khi
Câu 4:
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=3cos4x+4sin2x+√23sin4x+2cos2x+√2 Khi đó M+m=a+b√2, với a,b là các phân số tối giản. Ta có:
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=3cos4x+4sin2x+√23sin4x+2cos2x+√2 Khi đó M+m=a+b√2, với a,b là các phân số tối giản. Ta có:
Câu 6:
Đường cong hình vẽ bên mô tả đồ thị hàm số y=Asin(x+α)+B với A,B,α là các hằng số và α∈[0; π2]. Tính S=A+B+12απ.
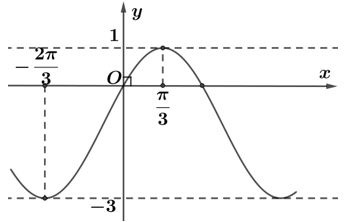
Đường cong hình vẽ bên mô tả đồ thị hàm số y=Asin(x+α)+B với A,B,α là các hằng số và α∈[0; π2]. Tính S=A+B+12απ.
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình x2+y2+2x−6y+1=0. Gọi (C') là ảnh của (C) qua phép vị tự tâm I(2;-3) tỉ số k = -2. Khi đó (C') có phương trình.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình x2+y2+2x−6y+1=0. Gọi (C') là ảnh của (C) qua phép vị tự tâm I(2;-3) tỉ số k = -2. Khi đó (C') có phương trình.
Câu 10:
Số nghiệm của phương trình cos22x+cos2x−34=0 trên khoảng (0;3π) là:
Số nghiệm của phương trình cos22x+cos2x−34=0 trên khoảng (0;3π) là:
Câu 11:
Cho đường tròn (O) và điểm P nằm trong đường tròn đó. Một đường thẳng thay đổi luôn đi qua P, cắt (O) tại hai điểm A và B. Khi đó, quỹ tích các điểm M thỏa mãn →PM=→PA+→PB là:
Cho đường tròn (O) và điểm P nằm trong đường tròn đó. Một đường thẳng thay đổi luôn đi qua P, cắt (O) tại hai điểm A và B. Khi đó, quỹ tích các điểm M thỏa mãn →PM=→PA+→PB là:
Câu 12:
Số vị trí biểu diễn các nghiệm của phương trình sin(2x−3)=cos(x+1) trên đường tròn lượng giác là
Số vị trí biểu diễn các nghiệm của phương trình sin(2x−3)=cos(x+1) trên đường tròn lượng giác là
Câu 13:
Cho hình chóp SABCD có đáy ABCD là hình thang (AB€CD,AB>CD). Gọi M,N lần lượt là trung điểm SB,SC. Khi đó mặt phẳng (AMN) cắt hình chóp SABCD theo thiết diện là
Cho hình chóp SABCD có đáy ABCD là hình thang (AB€CD,AB>CD). Gọi M,N lần lượt là trung điểm SB,SC. Khi đó mặt phẳng (AMN) cắt hình chóp SABCD theo thiết diện là
Câu 14:
Tính diện tích S của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các nghiệm của phương trình: 3(sinx+cos3x+sin3x1+2sin2x)=cos2x+2
Tính diện tích S của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các nghiệm của phương trình: 3(sinx+cos3x+sin3x1+2sin2x)=cos2x+2
Câu 15:
Nghiệm âm lớn nhất của phương trình tan2020x+cot2020x=2cos2019(π4−x)có dạng πabvới a,blà các số nguyên, a<0và a,bnguyên tố cùng nhau. Tính S = a+ b
Nghiệm âm lớn nhất của phương trình tan2020x+cot2020x=2cos2019(π4−x)có dạng πabvới a,blà các số nguyên, a<0và a,bnguyên tố cùng nhau. Tính S = a+ b


