Câu hỏi:
03/04/2024 36Có 3 quyển sách toán, 4 quyển sách lý và 5 quyển sách hóa khác nhau được sắp xếp ngẫu nhiên lên một giá sách có 3 ngăn, các quyển sách được sắp dựng đứng thành một hàng dọc vào một trong 3 ngăn ( mỗi ngăn đủ rộng để chứa tất cả các quyển sách). Tính xác suất để không có bất kỳ hai quyển sách toán nào đứng cạnh nhau.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
Tổng có 3 + 4 + 5 = 12 quyển sách được sắp xếp lên một giá sách có 3 ngăn (có 2 vách ngăn). Vì vậy, ta coi 2 vách ngăn này như 2 quyển sách giống nhau. Vậy số phần tử không gian mẫu ![]()
Gọi A là biến cố : “ Sắp xếp các 12 quyển sách lên giá sao cho không có bất kỳ hai quyển sách toán nào đứng cạnh nhau”.
+) Xếp 9 quyển sách ( lý và hóa) cùng 2 vách ngăn có cách
+) Lúc này, có 12 “khoảng trống” ( do 9 quyển sách ( lý và hóa) cùng 2 vách ngăn tạo ra) để xếp 3 quyển sách toán vào sao cho mỗi quyển vào một “khoảng trống” có cách.
Vậy có tất cả . cách. Suy ra 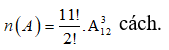
Vậy xác suất để không có bất kỳ hai quyển sách toán nào đứng cạnh nhau là:
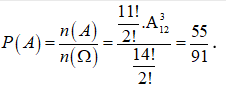
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Có hai dãy ghế đối diện nhau, mỗi dãy có năm ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ và bất kì hai học sinh ngồi liền kề nhau thì khác phái bằng
Câu 2:
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn đều là nữ
Câu 3:
Từ một hộp chứa 11 quả cầu màu đỏ và 4 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng
Câu 4:
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0;1;2;3;4;5;6;7;8;9. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn thỏa mãn abc
Câu 5:
Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 300. Gọi A là biến cố “số được chọn không chia hết cho 3”. Tính xác suất P(A) của biến cố A.
Câu 6:
Trong hệ trục tọa độ Oxy cho A(-2;0), B(-2;2), C(4;2), D(4;0). Chọn ngẫu nhiên một điểm có tọa độ (x;y) (với x, y ) nằm trong hình chữ nhật ABCD (kể cả các điểm trên cạnh). Gọi A là biến cố: “x, y đều chia hết cho 2”. Xác suất của biến cố A là .
Câu 7:
Một đề kiểm tra Toán Đại số và Giải tích chương 2 của khối 11 có 20 câu trắc nghiệm. Mỗi câu có 4 phương án lựa chọn, trong đó chỉ có 1 đáp án đúng. Mỗi câu trả lời đúng được 0,5 điểm và mỗi câu trả lời sai không được điểm nào. Một học sinh không học bài nên tích ngẫu nhiên câu trả lời. Tính xác suất để học sinh nhận được 6 điểm (kết quả làm tròn đến 4 chữ số sau dấu phẩy thập phân).
Câu 8:
Có 8 người khách bước ngẫu nhiên vào một cửa hàng có 3 quầy. Tính xác suất để 3 người cùng đến quầy thứ nhất.
Câu 9:
Gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp. Gọi a,b,c lần lượt là số chấm xuất hiện ở 3 lần gieo. Xác suất của biến cố “ số chia hết cho 45” là
Câu 10:
Trên giá sách có 4 quyển sách toán, 5 quyển sách lý. Lấy ngẫu nhiên ra 3 quyển sách. Tính xác suất để 3 quyển được lấy ra có ít nhất một quyển toán.
Câu 11:
Gọi S là tập tất cả các số tự nhiên gồm sáu chữ số được tạo thành từ các chữ số 1, 2, 3, 4, trong đó chữ số 1 có mặt đúng 3 lần, các chữ số còn lại mỗi chữ số có mặt đúng một lần. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn không có hai chữ số 1 nào đứng cạnh nhau.
Câu 12:
Trong một phòng học, có 36 cái bàn rời nhau được đánh số từ 1 đến 36, mỗi bàn dành cho 1 học sinh. Các bàn được xếp thành một hình vuông có kích thước 6x6. Cô giáo xếp tuỳ ý 36 học sinh của lớp vào các bàn, trong đó có hai bạn A và B. Xác suất để A và B ngồi ở hai bàn xếp cạnh nhau bằng (theo chiều ngang hoặc chiều dọc).
Câu 13:
Đội văn nghệ của một lớp có 5 bạn nam và 7 bạn nữ. Chọn ngẫu nhiên 5 bạn tham gia biểu diễn, xác suất để trong 5bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ bằng
Câu 14:
Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
Câu 15:
Có hai hộp đựng bi, mỗi viên bi chỉ mang một màu trắng hoặc đen. Lấy ngẫu nhiên từ mỗi hộp đúng một viên bi. Biết tổng số bi ở hai hộp là 20 và xác suất để lấy được hai viên bi đen là . Tính xác suất để lấy được hai viên bi trắng.


