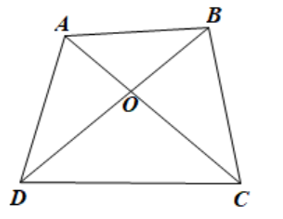
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng?

C. $\text{OA + OB + OC + OD < }\frac{\text{1}}{\text{2}}\left(\text{AB + BC + CD + DA}\right)$

Trả lời

Đáp án đúng là: A

Xét tam giác ABC:

$AB+BC>AC$ (bất đẳng thức tam giác)

Tương tự, lần lượt các tam giác BCD, CDA, DAB ta có:

$BC+CD>BD$

$CD+DA>CA$

$DA+AB>DB$

Cộng vế với vế ta được các bất đẳng thức trên ta được:

$AB+BC+CD+CD+DA+DA+AB>AC+BD+CA+DB$

$\iff 2\left(AB+BC+CD+DA\right)>2\left(AC+BD\right)$

$\iff AB+BC+CD+DA>AC+BD$

Mà: $AC+BD=OA+OC+OB+OD$ (hệ thức cộng đoạn thẳng)

$\iff OA+OB+OC+OD<AB+BC+CD+DA$

Vậy ta có:  $OA+OB+OC+OD<AB+BC+CD+DA$