Cho tứ giác ABCD có AB = BC, AD < CD. BD là phân giác của $\widehat{D}$  . Chứng minh $\widehat{A}+\widehat{C}=180°$  .

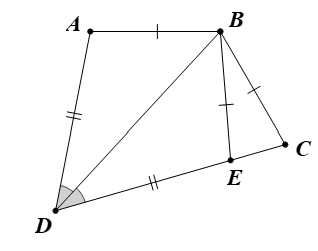
Trên cạnh CD, lấy điểm E sao cho DE = DA.

Xét ∆ABD và ∆EBD, có:

BD là cạnh chung;

DA = DE (giả thiết);

 $\widehat{ADB}=\widehat{EDB}$(do BD là phân giác của $\widehat{D}$  ).

Do đó ∆ABD = ∆EBD (c.g.c).

Suy ra AB = EB và $\widehat{BAD}=\widehat{BED}$  (cặp cạnh và cặp góc tương ứng).

Mà AB = BC (giả thiết)

Do đó EB = BC.

Vì vậy tam giác BCE cân tại B.

Suy ra $\widehat{BEC}=\widehat{BCE}$ .

Ta có  $\widehat{BAD}+\widehat{BCE}=\widehat{BED}+\widehat{BEC}=180°$(cặp góc kề bù).

Vậy $\widehat{A}+\widehat{C}=180°$ .