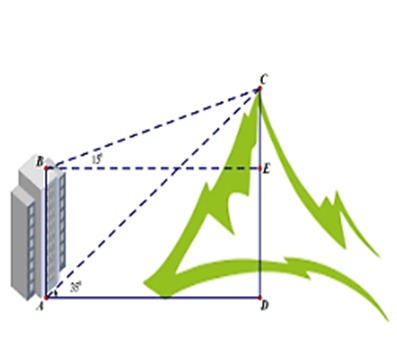
Một người quan sát đỉnh của một ngọn núi nhân tạo từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nằm ngang (như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao 60 m.

Ta có: \(\widehat {CBA} = \widehat {CBE} + \widehat {EBA} = 90^\circ + 15^\circ = 105^\circ \)

\(\widehat {BAC} = \widehat {BAD} - \widehat {CAD} = 90^\circ - 35^\circ = 55^\circ \)

Suy ra: \(\widehat {BCA} = 180^\circ - 55^\circ - 105^\circ = 20^\circ \)

Áp dụng định lý hàm sin cho tam giác CBA ta có:

\(\frac{{AB}}{{\sin \widehat {BCA}}} = \frac{{AC}}{{\sin \widehat {CBA}}}\)

Suy ra: \(AC = \frac{{AB.\sin \widehat {CBA}}}{{\sin \widehat {BCA}}} = \frac{{60.\sin 105^\circ }}{{\sin 20^\circ }} = 169,4506909\left( m \right)\)

Xét tam giác CAD vuông tại D ta có: CD = \(AC.\sin \widehat {CAD} \approx 97,193\left( m \right).\)